题目内容
已知:如图(1),⊙O1与⊙O2相交于A、B两点,经过A点的直线分别交⊙O1、⊙O2于C、D两点(C、D不与B重合),连结BD,过点C作BD的平行线交⊙O1于点E,连BE.
(1)求证:BE是⊙O2的切线;
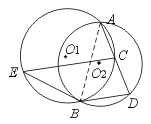
(2)如图(2),若两圆圆心在公共弦AB的同侧,其他条件不变,判断BE和⊙O2的位置关系(不要求证明).
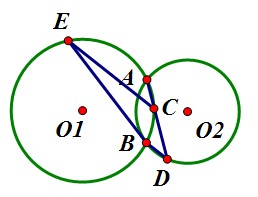
【证明】(1)连结AB,作⊙O2的直径BH,连结AH.
则 ∠ABH+∠H=90°,∠H=∠ADB,∠EBA=∠ECA.
 ∵ EC∥BD,
∵ EC∥BD,
∴ ∠ADB=∠ACE=∠EBA.
∴ ∠EBA+∠ABH=90°.
即 ∠EBH=90°.
∴ BE是⊙O2的切线.
(2)同理可知,BE仍是⊙O2的切线.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为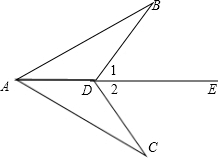 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为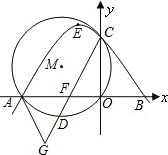 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧