题目内容
【题目】如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向中点F,G运动.连接PB,QE,设运动时间为t(s). 
(1)求证:四边形PEQB为平行四边形;
(2)填空: ①当t=s时,四边形PBQE为菱形;
②当t=s时,四边形PBQE为矩形.
【答案】
(1)证明:∵正六边形ABCDEF内接于⊙O,
∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF∠F,
∵点P,Q同时分别从A,D两点出发,以1cm/s速度,运动时间为t(s),
∴AP=DQ=t,则PF=QC=4﹣t,
在△ABP和△DEQ中
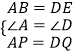
∴△ABP≌△DEQ(SAS)
∴BP=EQ,
同理可证,PE=QB,
∴四边形PEQB是平行四边形.
(2)2;0或4
【解析】(2)解:①当四边形PBQE为菱形时,PB=PE=EQ=QB, ∴△ABP≌△DEQ≌△PFE≌△QCB,
∴AP=PF=DQ=QC,
即t=4﹣t,得t=2,
故答案为:2;②当t=0时,∠EPF=∠PEF=30°,
∴∠BPE=120°﹣30°=90°,
∴此时四边形PBQE为矩形;
当t=4时,∠ABP=∠APB=30°,
∴∠BPE=120°﹣30°=90°,
∴此时四边形PBQE为矩形.
故答案为:0或4.
(1)根据正六边形ABCDEF内接于⊙O,可以得到正六边形的各边相等、各个内角相等,由点P,Q同时分别从A,D两点出发,以1cm/s速度,运动时间为t,可以得到BP与QE,PE与BQ的关系,从而可以证得结论;(2)①根据菱形的性质可以得到菱形的四条边都相等,从而可以得到所用的时间;②根据矩形的性质,可以分别得到t为多少时,四边形PBQE为矩形.

 名校课堂系列答案
名校课堂系列答案【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34



