题目内容
【题目】甲口袋中装有两个相同的小球，它们的标号分别为2和5，乙口袋中装有两个相同的小球，它们的标号分别为4和9，丙口袋中装有三个相同的小球，它们的标号分别为1，6，7．从这3个口袋中各随机取出一个小球．
（1）用树形图表示所有可能出现的结果；
（2）若用取出的三个小球的标号分别表示三条线段的长，求这些线段能构成三角形的概率．
【答案】
（1）解：如图所示：
，
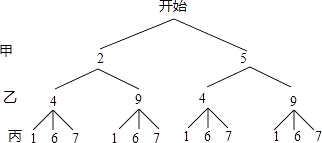所以共有12种可能出现的结果
（2）解：这些线段能够成三角形（记为事件A）的结果有4种：（5，4，6）；（5，4，7）；（5，9，6）（5，9，7），
所以P（A）= 
= 
【解析】（1）依据题意画树状图法分析所有等可能的出现结果即可解答；（2）根据树状图结合三角形的三边关系列举出能够成三角形的情况，用能够成三角形的情况数：总的情况数即可得到概率．
【考点精析】解答此题的关键在于理解三角形三边关系的相关知识，掌握三角形两边之和大于第三边；三角形两边之差小于第三边；不符合定理的三条线段，不能组成三角形的三边，以及对列表法与树状图法的理解，了解当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率．
练习册系列答案
相关题目
