题目内容
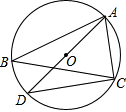（2012•河源二模）如图，⊙O是△ABC的外接圆，AD是⊙O的直径，连接CD，若⊙O的半径r=| 3 | 2 |
分析：先根据圆周角定理判断出△ACD的形状，由勾股定理求出CD的长，再根据∠B和∠D是同弧所对的圆周角∴∠B=∠D，由锐角三角形函数的定义即可得出结论．
解答：解：∵AD是⊙O的直径，y=
，
∴∠ACD=90°，
在Rt△ACD中，
∵AD=3，AC=2，
∴CD=
=
，
∴cosD=
，
∵∠B和∠D是同弧所对的圆周角，
∴∠B=∠D，
∴cosB=cosD=
．
| 3 |
| 2 |
∴∠ACD=90°，
在Rt△ACD中，
∵AD=3，AC=2，
∴CD=
| 32-22 |
| 5 |
∴cosD=
| ||
| 3 |
∵∠B和∠D是同弧所对的圆周角，
∴∠B=∠D，
∴cosB=cosD=
| ||
| 3 |
点评：本题考查的是圆周角定理，即在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
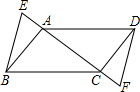（2012•河源二模）已知：如图，在?ABCD中，E是CA延长线上的点，F是AC延长线上的点，且AE=CF．求证：