题目内容
 如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=38°,则∠OAC的度数是( )
如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=38°,则∠OAC的度数是( )| A、38° | B、19° | C、76° | D、24° |
分析:根据平行线的性质可证∠OAC=∠ACB,又已知∠AOB=38°,可利用圆周角与圆心角的关系解得∠ACB,即可求∠OAC.
解答:解:∵AO∥BC,∠AOB=38°,
∴∠ACB=
∠AOB=
×38°=19°,
∴∠OAC=∠ACB=19°.
故选B.
∴∠ACB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OAC=∠ACB=19°.
故选B.
点评:本题考查的是圆周角与圆心角的关系即同弧或等弧所对的圆周角等于圆心角的一半及两直线平行的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
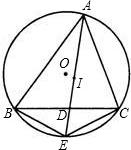 如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆OO于点E,连接BE、CE.
如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆OO于点E,连接BE、CE.

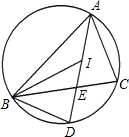 (2013•道外区三模)如图,点l是△ABC的内心,线段AI的延长线交△ABC外切圆于点D,交BC边于点E.
(2013•道外区三模)如图,点l是△ABC的内心,线段AI的延长线交△ABC外切圆于点D,交BC边于点E. 已知:如图,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A,B和C,D.求证:AB=CD.
已知:如图,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A,B和C,D.求证:AB=CD.