题目内容
【题目】如图,P为正方形ABCD内一点,PA=1,PB=2,PC=3.
(1)将△ABP绕点B顺时针旋转90°,得到△BEC,请你画出△BEC.
(2)连接PE,求证:△PEC是直角三角形;
(3)填空:∠APB的度数为 .

【答案】(1)详见解析;(2)详见解析;(3)135°.
【解析】
试题分析:(1)将△APB绕B点顺时针旋转90°,即将A,P,两点绕B点顺时针旋转90°,得出△CBE即可;(2)根据旋转的性质,得出∠PBE=∠ABC=90°,BP=BE=2,即可证得△PBE是等腰直角三角形,从而求得PE,最后根据勾股定理的逆定理,即可得到△PEC是直角三角形;(3)连接PE后,存在两个直角三角形:Rt△PBE和Rt△PCE,先求得∠BEC的度数,最后根据全等三角形的对应角相等,即可得出∠APB的度数.
试题解析:(1)如图所示,△CBE即为所求;
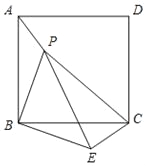
(2)证明:∵△BEC是由△APB绕点B顺时针方向旋转90°得到的,
∴△BEC≌△BPA,∠PBE=90°,
∴BE=BP=2,CE=PA=1,
∴△PBE是等腰直角三角形,CE2=1,
∴Rt△PBE中,PE2=PB2+BE2=4+4=8,
又∵PC=3,
∴PC2=9,
∴在△PCE中,PE2+CE2=PC2,
∴△PCE是直角三角形,且∠PEC=90°;
(3)由(2)可得,△PCE是直角三角形,△PBE是等腰直角三角形,
∴∠PEC=90°,∠BEP=45°,
∴∠BEC=90°+45°=135°,
又∵△BEC≌△BPA,
∴∠APB=∠BEC=135°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
