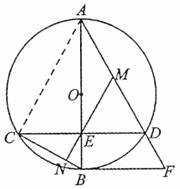
题目内容
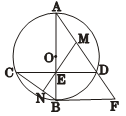
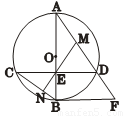
如图,![]() 为
为![]() 直径,且弦
直径,且弦![]() 于
于![]() ,过点
,过点![]() 的切线与
的切线与![]() 的延长线交于点
的延长线交于点![]() .
.
(1)若![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长
并延长![]() 交
交![]() 于
于![]() .求证:
.求证:![]() .
.
(2)若![]() ,求
,求![]() 的半径.
的半径.
 |
(1)(方法一)
连接![]() .
.
![]() 为
为![]() 的直径,且
的直径,且![]() 于
于![]() ,
,
由垂径定理得:点![]() 是
是![]() 的中点.
的中点.
又![]()
![]() 是
是![]() 的中点
的中点
![]() 是
是![]() 的中位线
的中位线
![]()
![]() 为
为![]() 直径,
直径,![]() ,
,
![]() 即
即![]()
(方法二)
![]() ,
,![]()
![]() 是
是![]() 的中点,
的中点,![]() ,即有
,即有![]()
又![]() ,由
,由![]() 与
与![]() 同对
同对![]() 知
知![]()
![]()
又![]()
![]()
![]() ,即
,即![]() .
.
(方法三)
![]() ,
,![]()
由于![]() 是
是![]() 的中点,
的中点,![]() ,即有
,即有![]()
又![]() 与
与![]() 同对
同对![]() ,
,![]()
又![]()
![]()
又![]()
![]()
即有![]() ,
,![]()
(2)连接![]()
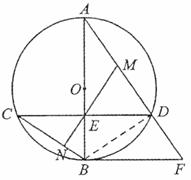
![]() 与
与![]() 同对
同对![]() ,
,![]()
![]()
![]() 为
为![]() 的切线,
的切线,![]()
在![]() 中,
中,![]()
设![]() ,则
,则![]() ,由勾股定理得:
,由勾股定理得:![]()
又![]() 为
为![]() 直径,
直径,![]()
![]()
![]()
即![]()
![]()
![]() 直径
直径![]()
则![]() 的半径为
的半径为![]()

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
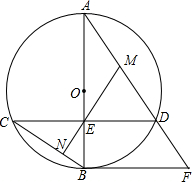 如图,AB为⊙O直径,且弦CD⊥AB于,过点的切线与AD的延长线交于点.
如图,AB为⊙O直径,且弦CD⊥AB于,过点的切线与AD的延长线交于点. 为
为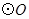 直径,且弦
直径,且弦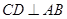 于
于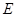 ,过点
,过点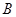 的切线与
的切线与 的延长线交于点
的延长线交于点 .
.
 是
是 并延长
并延长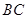 于
于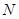 .求证:
.求证: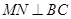 ;
;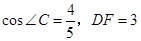 ,求
,求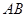 为
为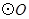 直径,且弦
直径,且弦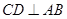 于
于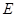 ,过点
,过点 的切线与
的切线与 的延长线交于点
的延长线交于点 .
.
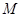 是
是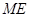 并延长
并延长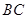 于
于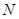 .求证:
.求证: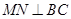 ;
;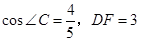 ,求
,求 (2)若cos∠C=
(2)若cos∠C=