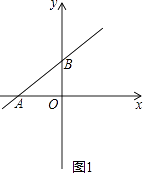题目内容
【题目】已知:在平面直角坐标系中,抛物线![]() 交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.

(1)求抛物线的解析式及顶点D的坐标.
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
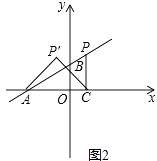
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
【答案】(1)y=﹣![]() (x+2)2+4,顶点D的坐标为(﹣2,4);(2)S=﹣2t+12,t=4时,S有最小值,最小值4;(3) 点P的坐标为(0,2).
(x+2)2+4,顶点D的坐标为(﹣2,4);(2)S=﹣2t+12,t=4时,S有最小值,最小值4;(3) 点P的坐标为(0,2).
【解析】(1)对称轴为x=﹣ =﹣2,
=﹣2,
解得b=﹣1,
所以,抛物线的解析式为y=﹣![]() x2﹣x+3,
x2﹣x+3,
∵y=﹣![]() x2﹣x+3=﹣
x2﹣x+3=﹣![]() (x+2)2+4,
(x+2)2+4,
∴顶点D的坐标为(﹣2,4);
(2)令y=0,则﹣![]() x2﹣x+3=0,
x2﹣x+3=0,
整理得,x2+4x﹣12=0,
解得x1=﹣6,x2=2,
∴点A(﹣6,0),B(2,0),
如图1,过点D作DE⊥y轴于E,
∵0≤t≤4,
∴△PAD的面积为S=S梯形AOED﹣S△AOP﹣S△PDE,
=![]() ×(2+6)×4﹣
×(2+6)×4﹣![]() ×6t﹣
×6t﹣![]() ×2×(4﹣t),
×2×(4﹣t),
=﹣2t+12,
∵k=﹣2<0,
∴S随t的增大而减小,
∴t=4时,S有最小值,最小值为﹣2×4+12=4;
(3)如图2,过点D作DF⊥x轴于F,
∵A(﹣6,0),D(﹣2,4),
∴AF=﹣2﹣(﹣6)=4,
∴AF=DF,
∴△ADF是等腰直角三角形,
∴∠ADF=45°,
由二次函数对称性,∠BDF=∠ADF=45°,
∴∠PDA=90°时点P为BD与y轴的交点,
∵OF=OB=2,
∴PO为△BDF的中位线,
∴OP=![]() DF=2,
DF=2,
∴点P的坐标为(0,2),
由勾股定理得,DP=![]() =2
=2![]() ,
,
AD=![]() AF=4
AF=4![]() ,
,
∴![]() =
=![]() =2,
=2,
令x=0,则y=3,
∴点C的坐标为(0,3),OC=3,
∴![]() =
=![]() =2,
=2,
∴![]() =
=![]() ,
,
又∵∠PDA=90°,∠COA=90°,
∴Rt△ADP∽Rt△AOC.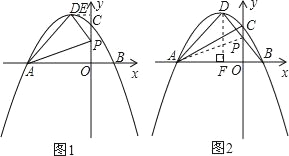

 阅读快车系列答案
阅读快车系列答案【题目】甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级 | 参赛人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
某同学分析上表后得出如下结论:
①甲、乙两班学生成绩平均水平相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
③甲班成绩的波动比乙班大,
上述结论正确的是( )
A.①②③
B.①②
C.①③
D.②③