题目内容
 (1)计算:
(1)计算: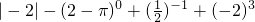 ;
;
(2)先将: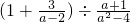 化简,然后请自选一个你喜欢的x值,再求原式的值;
化简,然后请自选一个你喜欢的x值,再求原式的值;
(3)已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F.求证:AB=FC.
(1)解:原式=2-1+2-8
=-5;
(2)解:原式=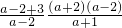
= •
•
=a+2;
∵a-2≠0,a+1≠0,a2-4≠0,
∴a的值不能为±2和1,
取a=0,原式=0+2=2;
(3)证明:∵EF⊥AC于点E,∠ACB=90°,
∴∠FEC=∠ACB=90°
∴∠F+∠ECF=90°
又∵CD⊥AB于点D,
∴∠A+∠ECF=90°
∴∠A=∠F,
在△ABC和△FCE中,
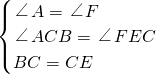 ,
,
∴△ABC≌△FCE (AAS),
∴AB=FC.
分析:(1)根据绝对值,零指数幂,负整数指数幂,正整数指数幂分别求出每一部分的值,再代入求出即可;
(1)先算括号内的减法,同时把除法变成乘法,再算乘法,最后代入求出即可;
(3)求出∠A=∠F,∠ACB=∠FEC,根据AAS证△ACB≌△FEC,根据全等三角形的性质推出即可.
点评:本题考查了全等三角形的性质和判定,负整数指数幂,分式的混合运算,绝对值,三角形的内角和定理,零指数幂,实数的运算等知识点的综合运用.
=-5;
(2)解:原式=
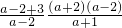
=
 •
•
=a+2;
∵a-2≠0,a+1≠0,a2-4≠0,
∴a的值不能为±2和1,
取a=0,原式=0+2=2;
(3)证明:∵EF⊥AC于点E,∠ACB=90°,

∴∠FEC=∠ACB=90°
∴∠F+∠ECF=90°
又∵CD⊥AB于点D,
∴∠A+∠ECF=90°
∴∠A=∠F,
在△ABC和△FCE中,
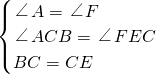 ,
,∴△ABC≌△FCE (AAS),
∴AB=FC.
分析:(1)根据绝对值,零指数幂,负整数指数幂,正整数指数幂分别求出每一部分的值,再代入求出即可;
(1)先算括号内的减法,同时把除法变成乘法,再算乘法,最后代入求出即可;
(3)求出∠A=∠F,∠ACB=∠FEC,根据AAS证△ACB≌△FEC,根据全等三角形的性质推出即可.
点评:本题考查了全等三角形的性质和判定,负整数指数幂,分式的混合运算,绝对值,三角形的内角和定理,零指数幂,实数的运算等知识点的综合运用.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目