题目内容
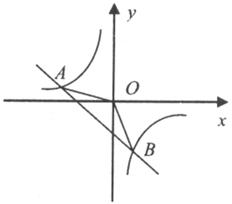
反比例函数
的图像如下图所示，点M是该函数图像上一点，MN垂直于
轴，垂足是点N，如果S△MON=2，则k的值为 ．
一4
练习册系列答案
相关题目
(k≠0)任取一点M(a，b)，过M作MA⊥x轴，MB⊥y轴，所得矩形OAMB的面积为S＝MA·MB＝|b|·|a|＝|ab|．又因为b＝
，故ab＝k，所以S＝|k|(如图(1))．
(k＜0)的图像上，试比较矩形P1AOB与矩形P2COD的面积大小．
＝|k|
＝|k|
(x＞0)的图像上有三点A、B、C，经过三点分别向x轴引垂线，交x轴于A1、B1、C1三点，连结OA、OB、OC，记△OAA1、△OBB1、△OCC1的面积分别为S1、S2、S3，则有( )
＝
|k|＝
＝
＝
|k|
．
(x＞0)的图像上任意两点A、B分别作轴和垂线，垂足分别为C、D，连结OA、OB，设AC与OB的交点为E，△AOE与梯形ECDB的面积分别为S1、S2，比较它们的大小，可得
北京红螺食品公司生产的各种果脯一直受到大众的喜爱，尤其是该公司生产的桃脯特别香甜可口.但由于该公司某经销点存货有限，在2011年1到5月该经销点每月桃脯的销量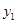
（千克）与月份
的关系如下表所示：
| （月） | 1 | 2 | 3 | 4 | 5 |
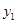| （千克） | 150 | 75 | 50 | 37.5 | 30 |
6月份由于鲜桃的大量上市，红螺公司进行大量采购与加工，所以在6到12月该经销点每月桃脯的销量
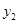（千克）与月份
的函数关系为：
；已知在1到5月该经销点每千克桃脯的价格
（元）与月份
的函数关系为：
；而在6到12月每千克桃脯的价格
（元）与月份的关系满足如下函数图像；
（1）请观察图中的表格，用所学过的一次函数、反比例函数、二次函数的有关知识直接写出
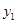与的函数关系式，根据如图所示的变换趋势，直接写出与之间满足的一次函数关系式，并注明x的取值范围；（2）试求出该经销点在哪个月桃脯的销售额最大，最大为多少元；
（3）为满足市场所需，红螺公司决定在2012年将此种桃脯作为海外出口的首推品，所以在今年1到4月该经销点在去年获得最大销售额的基础上，每月的总销量都上涨了
，且其中的
是用于出口，剩余部分由经销点国内销售，每月出口桃脯的售价每千克降低了
，而国内销售的桃脯价格每千克上涨了
，这样该经销点1到4月销售桃脯的总额为142560元，试求出
的值. （参考数据：
， 
， 
， 
） 
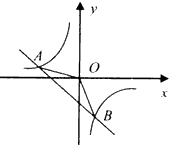
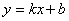的图像与反比例函数
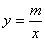的图像交于A（-2，1），B（1，
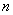）两点。 
的图像上，过点M作ME⊥
轴，过点N作NF⊥
轴，垂足分别为E，F。试证明：MN∥EF。
的图像与反比例函数
的图像交于A（－2，1），B（1，
）两点。