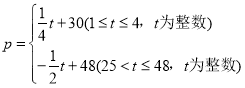ћвƒњƒЏ»Ё
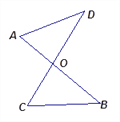
°Њћвƒњ°њ»зЌЉ£ЇѕяґќAB°ҐCDѕаљї”ЏµгO£ђЅђљ”AD°ҐCB£ђќ“√«∞—’вЄцЌЉ–ќ≥∆ќ™°∞8„÷–Ќ°±.
ЄщЊЁ»эљ«–ќƒЏљ«ЇЌ»Ё“„µ√µљ£Ї°ѕA+°ѕD=°ѕC+°ѕB.
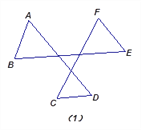
Ґ≈јы”√°∞8„÷–Ќ°±
»зЌЉ£®1£©£Ї°ѕA+°ѕB+°ѕC+°ѕD+°ѕE+°ѕF=_________.
Ґ∆єє‘м°∞8„÷–Ќ°±
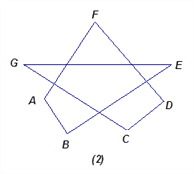
»зЌЉ£®2£©£Ї°ѕA+°ѕB+°ѕC+°ѕD+°ѕE+°ѕF+°ѕG=_________.
Ґ«ЈҐѕ÷°∞8„÷–Ќ°±
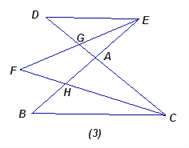
»зЌЉ£®3£©£ЇBE°ҐCDѕаљї”ЏµгA£ђCFќ™°ѕBCDµƒ∆љЈ÷ѕя£ђEFќ™°ѕBEDµƒ∆љЈ÷ѕя.
ҐўЌЉ÷–є≤”–________Єц°∞8„÷–Ќ°±£ї
ҐЏ»ф°ѕB£Ї°ѕD£Ї°ѕF=4£Ї6£Їx£ђ«уxµƒ÷µ£Ѓ
°Њір∞Є°њ 360 540ґ» Ґў6
°Њљвќц°њ£®1£©»зЌЉ£ђ
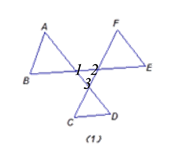
”…°∞8„÷–Ќ°±µ√£ђ°ѕA+°ѕB=°ѕ2+°ѕ3Ґў; °ѕC+°ѕD=°ѕ2+°ѕ1ҐЏ;°ѕE+°ѕF=°ѕ1+°ѕ3Ґџ£ї
+ҐЏ+Ґџµ√
°ѕA+°ѕB+°ѕC+°ѕD+°ѕE+°ѕF=2£®°ѕ1+°ѕ2+°ѕ3£©=360°г.
£®2£©»зЌЉ£ђЅђљ”BC.
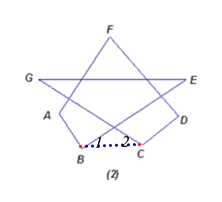
°я°ѕA+°ѕABE+°ѕ1+°ѕ2+°ѕDCG+°ѕD+°ѕF=540°г; °ѕ1+°ѕ2=°ѕG+°ѕE;
°а°ѕA+°ѕABE+°ѕG+°ѕE+°ѕDCG+°ѕD+°ѕF=540°г.
£®3£©ҐўЌЉ÷–”–6Єц°∞8„÷–Ќ°±£ї
ҐЏ»зЌЉ£ђ
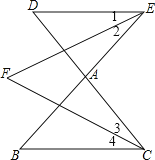
°яCFќ™°ѕBCDµƒ∆љЈ÷ѕя£ђEFќ™°ѕBEDµƒ∆љЈ÷ѕя£ђ
°а°ѕ1=°ѕ2£ђ°ѕ3=°ѕ4£ђ
°я°ѕD+°ѕ1=°ѕF+°ѕ3£ђ
°ѕB+°ѕ4=°ѕF+°ѕ2£ђ
°а°ѕB+°ѕD+°ѕ1+°ѕ4=2°ѕF+°ѕ3+°ѕ2£ђ
![]() £ї
£ї
µ±°ѕB:°ѕD:°ѕF=4:6:x ±£ђ…и°ѕB=4a£ђ‘т°ѕD=6a£ђ°ѕF=ax£ђ
°я2°ѕF=°ѕB+°ѕD£ђ
°а2ax=4a+6a
°а2x=4+6£ђ
°аx=5.