题目内容
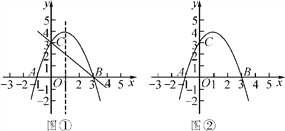
【题目】如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.

(1)求点E的坐标;
(2)求折痕CD所在直线的函数表达式;
(3)请你延长直线CD交x轴于点F. ①求△COF的面积;
②在x轴上是否存在点P,使S△OCP=![]() S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)E(8,0);
(2)y=﹣![]() x+6
x+6
(3)①54;②点P的坐标为(6,0)或(﹣6,0).
【解析】(1)根据折叠的性质知CE=CB=10.在在直角△COE中,由勾股定理求得OE=8;
(2)根据OC=6知C(0,6),由折叠的性质与勾股定理,求得D(10,![]() ),利用待定系数法求CD所在直线的解析式;
),利用待定系数法求CD所在直线的解析式;
(3)①根据F(18,0),即可求得△COF的面积;②设P(x,0),依S△OCP=![]() S△CDE得
S△CDE得![]() ×OP×OC=
×OP×OC=![]() ×54,即
×54,即![]() ×|x|×6=18,求得x的值,即可得出点P的坐标.
×|x|×6=18,求得x的值,即可得出点P的坐标.
(1)如图,

∵四边形ABCD是长方形,
∴BC=OA=10,∠COA=90°,
由折叠的性质知,CE=CB=10,
∵OC=6,
∴在直角△COE中,由勾股定理得OE=![]() =8,
=8,
∴E(8,0);
(2)设CD所在直线的解析式为y=kx+b(k≠0),
∵C(0,6),
∴b=6,
设BD=DE=x,
∴AD=6-x,AE=OA-OE=2,
由勾股定理得AD2+AE2=DE2
即(6-x)2+22=x2,
解得x=![]() ,
,
∴AD=6-![]() =
=![]() ,
,
∴D(10,![]() ),
),
代入y=kx+6 得,k=-![]() ,
,
故CD所在直线的解析式为:y=-![]() x+6;
x+6;
(3)①在y=-![]() x+6中,令y=0,则x=18,
x+6中,令y=0,则x=18,
∴F(18,0),
∴△COF的面积=![]() ×OF×OC=
×OF×OC=![]() ×18×6=54;
×18×6=54;
②在x轴上存在点P,使得S△OCP=![]() S△COF,
S△COF,
设P(x,0),依题意得
![]() ×OP×OC=
×OP×OC=![]() ×54,即
×54,即![]() ×|x|×6=18,
×|x|×6=18,
解得x=±6,
∴在x轴上存在点P,使得S△OCP=![]() S△COF,点P的坐标为(6,0)或(-6,0).
S△COF,点P的坐标为(6,0)或(-6,0).

【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?