题目内容
【题目】如图，已知抛物线y=mx2+2mx+c（m≠0），与y轴交于点C（0，﹣4），与x轴交于点A（﹣4，0）和点B．
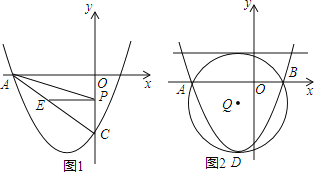
（1）求该抛物线的解析式；
（2）若P是线段OC上的动点，过点P作PE∥OA，交AC于点E，连接AP，当△AEP的面积最大时，求此时点P的坐标；
（3）点D为该抛物线的顶点，⊙Q为△ABD的外接圆，求证⊙Q与直线y=2相切．
【答案】（1）y=
x2+x﹣4．（2）P（0，﹣2）；（3）见解析
【解析】
试题分析：审题知：（1）题中已知抛物线上的两个点，只需将点坐标代入抛物线解析式即可求解；
（2）此题只需设出点P的坐标（0，t），并根据题中关系，列出△AEP面积关于t的二次函数即可求解；
（3）此题应先求出圆心Q的坐标，在求出半径，证明圆心到直线的距离等于半径即可．
解：（1）把点C（0，﹣4），点A（﹣4，0）坐标代入：y=mx2+2mx+c（m≠0）得：
，
解得：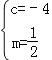
．
所以：抛物线的解析式为：y=x2+x﹣4．
（2）设点P（0，t）﹣4≤t≤0，则有：PC=t+4，OP=﹣t，OA=4
由PE∥OA可知：三角形CPE，三角形POA，三角形AOC均为直角三角形，
所以：
，
，解得：PE=t+4
所以：S△AEP=×OA×OC﹣×OA×OP﹣×PC×PE
=×4×4﹣×4×（﹣t）﹣×（t+4）×（t+4）
=﹣t2﹣2t．
所以：当t=﹣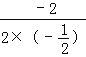
=﹣2时，△AEP的面积最大，
此时：P（0，﹣2）；
（3）过点D作DM⊥x轴，垂足为M，
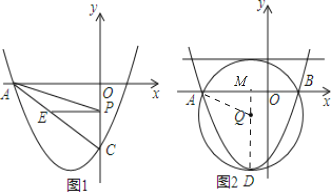
抛物线的解析式为：y=
x2+x﹣4=（x+1）2﹣
所以：顶点D（﹣1，），点M（﹣1，0），AM=﹣1﹣（﹣4）=3
由圆和抛物线的对称性可知：圆心Q在DM上，QM⊥AB，
设圆Q的半径为r，则AQ=r，QM=﹣r，由勾股定理得：
r2=
+32，解得：r=
，QM=
﹣r=
，所以点Q（﹣1，﹣）
因为直线y=2与x轴平行，所以点Q到直线y=2的距离为：2﹣（﹣）=，
所以：圆心Q到直线y=2的距离=圆的半径
所以：⊙Q与直线y=2相切．
