题目内容
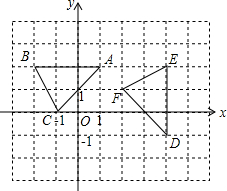 如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是( )
如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是( )| A、(0,0) |
| B、(1,0) |
| C、(1,-1) |
| D、(2.5,0.5) |
考点:坐标与图形变化-旋转
专题:数形结合
分析:先根据旋转的性质得到点A的对应点为点D,点B的对应点为点E,再根据旋转的性质得到旋转中心在线段AD的垂直平分线,也在线段BE的垂直平分线,即两垂直平分线的交点为旋转中心,而易得线段BE的垂直平分线为直线x=1,线段AD的垂直平分线为以AD为对角线的正方形的另一条对角线所在的直线.
解答:解:∵将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,
∴点A的对应点为点D,点B的对应点为点E,
作线段AD和BE的垂直平分线,它们的交点为P(1,-1),
∴旋转中心的坐标为(1,-1).
故选C.
∴点A的对应点为点D,点B的对应点为点E,
作线段AD和BE的垂直平分线,它们的交点为P(1,-1),
∴旋转中心的坐标为(1,-1).
故选C.
点评:本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若二次函数y=x2+2x+c配方后为y=(x+h)2+7,则c、h的值分别为( )
| A、8、-1 | B、8、1 |
| C、6、-1 | D、6、1 |
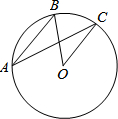 如图,A、B、C在⊙O上,若∠BAC=24°,则∠BOC的度数是( )
如图,A、B、C在⊙O上,若∠BAC=24°,则∠BOC的度数是( )| A、12° | B、24° |
| C、48° | D、84° |
二次函数y=2(x+1)2-3的最小值是( )
| A、1 | B、-1 | C、3 | D、-3 |
下列说法正确的是( )
| A、“明天降雨的概率是80%”表示明天有80%的时间降雨 |
| B、“一批铅笔的废品率为0.1%”表示如果从中抽出一只铅笔肯定不是废品 |
| C、“彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖 |
| D、在同一年出生的367名学生中,至少有两人的生日是同一天 |
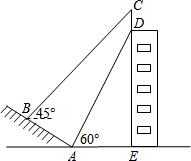 如图,某校一幢教学大楼的顶部竖有一块中考倒计时牌CD.小明在山坡的坡脚A处测得倒计时牌底部D的仰角为60°,沿山坡向上走到B处测得倒计时牌顶部C的仰角为45°.已知山坡AB的坡度i=1:
如图,某校一幢教学大楼的顶部竖有一块中考倒计时牌CD.小明在山坡的坡脚A处测得倒计时牌底部D的仰角为60°,沿山坡向上走到B处测得倒计时牌顶部C的仰角为45°.已知山坡AB的坡度i=1: