题目内容
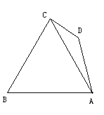
【题目】四边形ABCD中，BC⊥CD，∠BCA＝600，∠CDA＝1350，
。求AD边的长.
【答案】8
【解析】
作AF⊥AC于F，作AE⊥CD交CD的延长线于E，利用三角形的面积公式S△ABC=
BCAF求得AF的长，在△AFC中，根据∠BCA的正弦求得AC的长，再证明△ADE为等腰直角三角形，由此即可求解．
作AF⊥AC于F，作AE⊥CD交CD的延长线于E。可求AC＝16，AD＝8.
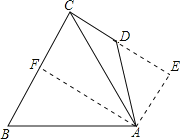
作AF⊥BC于F，作AE⊥CD交CD的延长线于E．
∵S△ABC=BCAF=×10×AF=40
，
∴AF=8，
∵sin∠BCA=sin60°=AF：AC=
，
∴AC=16．
∵BC⊥CD，AE⊥CD
∴∠CAE=∠BCA=60°，
∴∠ACD=90°-60°=30°，
∵∠CDA=135°，
∴AE=ED=sin∠ACDAC=8．
在等腰直角三角形中AD=AE=8．
练习册系列答案
相关题目
