(6分)探究做功与速度变化的关系实验中,某同学利用如图所示的装置,通过数根相同的橡皮条和打点计时器,来探究橡皮条做功与小车获得速度之间的关系,得到下面数据,
| A | B | C |
| 橡皮条数 | 速度 | 速度的平方 |
| 1 | 1.00 | 1.00 |
| 2 | 1.41 | 1.99 |
| 3 | 1.73 | 2.99 |
| 4 | 2.00 | 4.00 |
| A.利用改变橡皮条的根数来改变做功的大小,使做功数值倍数增加 |
| B.每次改变橡皮条的根数,必须将小车拉到相同位置由静止释放 |
| C.从表格A 列和B列对比,可以判断橡皮筋做功与小车速度成正比例关系 |
| D.从表格 A 列和C列对比,可以判断橡皮筋做功与小车速度平方成正比例关系 |
在“利用单摆测重力加速度”的实验中:
(1)以下做法中正确的是( )
| A.测量摆长的方法:用刻度尺量出从悬点到摆球间的细线长 |
| B.测量周期时,从小球到达最大振幅位置开始计时,摆球完成50次全振动时,及时截止,然后求出完成一次全振动的时间 |
| C.要保证单摆自始至终在同一竖直面内摆动 |
| D.单摆振动时,应注意使它的偏角开始时不能小于10° |
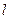 和周期T计算重力加速度的公式是g= 。
和周期T计算重力加速度的公式是g= 。(3)实验中,如果摆球密度不均匀,无法确定重心位置,一位同学设计了一个巧妙的方
法不计摆球的半径。具体做法如下:第一次量得悬线长L1,测得振动周期为T1;第二次
量得悬线长L2,测得振动周期为T2,由此可推得重力加速度为g= 。
(10分)某实验小组设计了如图a所示的实验装置,用钩码所受重力作为小车所受的拉力,用DIS测小车的加速度.通过改变钩码的数量,多次重复测量,可得小车运动的加速度a和所受拉力F的关系图像.他们在轨道水平和倾斜的两种情况下分别做实验,得到了两条a-F图线,如图b所示.
(1)图线 是在轨道右侧抬高成为斜面情况下得到的.(选填“①”或“②”)
(2)随着钩码的数量增大到一定程度时图b中的图线明显偏离直线,造成此误差的主要原因是所挂钩码的总质量太大,为消除此误差可采取的最为简便且有效的措施是
| A.调整轨道的倾角,在未挂钩码时使小车能在轨道上长时间缓慢运动(即小车与传感器发射部分的重力沿轨道方向的分力恰与其所受摩擦力平衡) |
| B.在增加钩码数量进行实验的同时在小车上增加砝码,使钩码的总质量始终远小于小车与传感器接收部分的总质量 |
| C.在钩码与细绳之间放置一力传感器,直接得到小车运动的加速度a和力传感器读数F的关系图像 |
| D.更换实验中使用的钩码规格,采用质量较小的钩码进行上述实验 |
(13分)(1)某同学在用单摆测定重力加速度的实验中,测量5种不同摆长情况下单摆的振动周期,记录表格如下:
| 摆长L(m) | 0.5 | 0.8 | 0.9 | 1.0 | 1.2 |
| 周期T(s) | 1.42 | 1.79 | 1.90 | 2.00 | 2.20 |
| T2(s2) | 2.02 | 3.20 | 3.61 | 4.00 | 4.84 |
 。
。②.若通过计算测得重力加速度g的值偏大,
其原因可能是 ▲
| A.摆球质量太大 |
| B.单摆振幅偏小 |
| C.误将n次全振动记录为(n+1)次 |
| D.误将摆线长当成摆长,未加小球的半径 |

(2).右图是一个单摆在淮州中学实验室做受迫振动时的共振曲线。
①.该单摆的摆长
 ▲
▲  (取
(取 )
)②.若用摆长相同的单摆装置分别在淮州中学、北京大学实验室做相同的受迫振动实验,则在北京大学实验室得到的共振曲线与上图比较:共振曲线的“峰” ▲ (填“向左移动”、“保持不变”或“向右移动”)



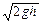 计算与C点对应的重锤的瞬时速度,得到动能的增加量,这种做法 (填“对”或“不对”)
计算与C点对应的重锤的瞬时速度,得到动能的增加量,这种做法 (填“对”或“不对”)


 =L2,小滑块与两个平面的动摩擦因数相同,又以上数据可以求出物块与平面间的动摩擦因数μ= 。
=L2,小滑块与两个平面的动摩擦因数相同,又以上数据可以求出物块与平面间的动摩擦因数μ= 。
