题目内容
8.如图所示,AB长L0=2m的粗糙水平轨道,MD为光滑水平轨道,圆O为半径R=0.45m的下端不闭合的竖直光滑圆轨道,它的入口和出口分别为AB和MD在B、M两点水平平滑连接.D点右侧有一宽x0=0.9m的壕沟,壕沟右侧的水平面EG比轨遭MD低h=0.45m.质量m=0.2kg的小车(可视为质点)能在轨道上运动.空气阻力不计,g取10m/s2.(1)将小车至于D点静止,为使小车能越过壕沟,至少要使小车具有多大的水平初速度?
(2)将小车至于A点静止,用F=1.9N的水平恒力向右拉小车,F作用的距离最大不超过2m,小车在AB轨道上受到的摩擦力恒为f=0.3N,为使小车通过圆轨道完成圆周运动进入MD轨道后,能够从D点越过壕沟,力F的作用时间应该满足什么条件?

分析 (1)根据平抛运动的高度求出平抛运动的时间,结合最小水平距离得出初速度的范围.
(2)根据牛顿第二定理求出最高点的最小速度,结合动能定理求出最低点M的速度,从而判断出满足通过壕沟以及通过最高点的条件,结合动能定理求出F作用的最小距离,根据牛顿第二定律和运动学公式求出作用的最短时间,根据F作用的最大路程求出F作用的最长时间.
解答 解:(1)根据h=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×0.45}{10}}s=0.3s$,
则小车具有的最小初速度${v}_{0}=\frac{{x}_{0}}{t}=\frac{0.9}{0.3}m/s=3m/s$.
(2)小球通过最高点的最小速度${v}_{1}=\sqrt{gR}=\sqrt{10×0.45}$m/s=$\sqrt{4.5}m/s$,
根据动能定理知,$mg•2R=\frac{1}{2}m{{v}_{M}}^{2}-\frac{1}{2}m{{v}_{1}}^{2}$,
代入数据解得vM=$\sqrt{13.5}$m/s>3m/s,
可知小球能够通过最高点,则能通过壕沟,
对A到C的过程运用动能定理得,$Fx-f{L}_{0}-mg•2R=\frac{1}{2}m{{v}_{1}}^{2}-0$,
代入数据解得x=1.5m,
根据牛顿第二定律得,a=$\frac{F-f}{m}=\frac{1.9-0.3}{0.2}m/{s}^{2}=8m/{s}^{2}$,
根据x=$\frac{1}{2}a{t′}^{2}$得,力F作用的最短时间$t′=\sqrt{\frac{2x}{a}}=\sqrt{\frac{2×1.5}{8}}s≈0.6s$,
力F作用的最长时间$t″=\sqrt{\frac{2{L}_{0}}{a}}=\sqrt{\frac{2×2}{8}}s≈0.7s$,
则力F的作用时间应该满足0.6s≤t≤0.7s.
答:(1)至少要使小车具有3m/s的水平初速度;
(2)力F的作用时间应该满足0.6s≤t≤0.7s.
点评 本题考查了平抛运动和圆周运动的综合运用,知道平抛运动在水平方向和竖直方向上的运动规律以及圆周运动向心力的来源是解决本题的关键.

| A. | 由E=$\frac{F}{q}$可知,若q减半,则该处场强为原来的2倍 | |
| B. | 公式E=$\frac{{U}_{ab}}{d}$适用于计算任何电场中a、b两点间的电势差 | |
| C. | 由E=k$\frac{Q}{{r}^{2}}$可知,真空中点电荷周围某点的场强由Q和r共同决定 | |
| D. | 由E=k$\frac{Q}{{r}^{2}}$可知,与场源电荷距离相等的点的场强相同 |
| A. | 质点是为了研究问题方便而忽略次要因素的一种理想化模型 | |
| B. | 伽利略利用实验结合逻辑推理的方法得出了力和运动的关系 | |
| C. | 利用多次测量取平均值的方法可有效减小实验的系统误差 | |
| D. | 将平抛运动分解为两个方向的直线运动是等效替代的方法 |
 把一个小球放在光滑的玻璃漏斗中,晃动漏斗,可使小球沿漏斗壁在某一水平面内做匀速圆周运动.如图所示,关于小球的受力情况,下列说法正确的是( )
把一个小球放在光滑的玻璃漏斗中,晃动漏斗,可使小球沿漏斗壁在某一水平面内做匀速圆周运动.如图所示,关于小球的受力情况,下列说法正确的是( )| A. | 小球受到重力、漏斗壁的支持力2个力 | |
| B. | 小球受到重力、漏斗壁的支持力及向心力3个力 | |
| C. | 小球受到重力、漏斗壁的支持力、摩擦力及向心力4个力 | |
| D. | 小球受到的合力为零 |
 如图所示.斜面OAB的倾角为θ,放在水平地面上,现从顶点O以速度v0平抛一小球,恰好落在斜面的最低点.不计空气阻力,重力加速度为g,则( )
如图所示.斜面OAB的倾角为θ,放在水平地面上,现从顶点O以速度v0平抛一小球,恰好落在斜面的最低点.不计空气阻力,重力加速度为g,则( )| A. | 小球落到斜面上的时间为$\frac{{v}_{0}tanθ}{g}$ | |
| B. | 小球落到斜面上时速度方向与水平方向的夹角为α,则α=2θ | |
| C. | 小球落到斜面上时速度方向与水平方向的夹角为α,则tanα=2tanθ | |
| D. | 小球在飞行过程中离斜面最远时所用的时间为$\frac{2{v}_{0}tanθ}{g}$ |
 如图所示,一束复色光由空气射向玻璃,发生折射而分为a、b两束单色光.设玻璃对a、b的折射率分别为na和nb,a、b在玻璃中的传播速度分别为va和vb.则( )
如图所示,一束复色光由空气射向玻璃,发生折射而分为a、b两束单色光.设玻璃对a、b的折射率分别为na和nb,a、b在玻璃中的传播速度分别为va和vb.则( )| A. | na>nb,va<vb | B. | na<nb,va<vb | C. | na<nb,va>vb | D. | na<nb,va<vb |
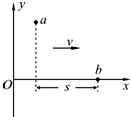 如图所示,a、b是一列横波上的两个质点,它们在x轴上的距离s=30m,波沿x轴正方向传播,当a振动到最高点时b恰好经过平衡位置向上振动,经过3s波传播了30m,下列判断正确的是( )
如图所示,a、b是一列横波上的两个质点,它们在x轴上的距离s=30m,波沿x轴正方向传播,当a振动到最高点时b恰好经过平衡位置向上振动,经过3s波传播了30m,下列判断正确的是( )| A. | 这列波的速度一定是10m/s | B. | 这列波的周期一定是0.8s | ||
| C. | 这列波的周期可能是3s | D. | 这列波的波长可能是24m |
