题目内容
20.已知下面的数据,可以求出地球质量M的是(引力常数G是已知的)( )| A. | 人造地球卫星在地面附近的运行速度v和运行周期T3 | |
| B. | 地球“同步卫星”离地面的高度h | |
| C. | 地球绕太阳运行的周期T2及地球到太阳中心的距离R2 | |
| D. | 月球绕地球运行的周期T1及月球到地球表面的距离R1 |
分析 万有引力的应用之一就是计算中心天体的质量,计算原理就是万有引力提供球绕天体圆周运动的向心力,列式只能计算中心天体的质量.
解答 解:A、人造地球卫星绕地球做圆周运动,地球对卫星的万有引力提供卫星做圆周运动的向心力
$G\frac{Mm}{{R}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{3}^{2}}R$,可得地球的质量$M=\frac{4{π}_{\;}^{2}{R}_{\;}^{3}}{G{T}_{3}^{2}}$①
根据卫星线速度的定义可知$v=\frac{2πR}{{T}_{3}^{\;}}$得$R=\frac{v{T}_{3}^{\;}}{2π}$②
②代入①得$M=\frac{{v}_{\;}^{3}{T}_{3}^{\;}}{2πG}$,故A正确;
B、地球“同步卫星”绕地球做匀速圆周运动的周期等于地球的自转周期,即T=24h,根据万有引力提供向心力$G\frac{Mm}{(R+h)_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}(R+h)$,可得地球质量$M=\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}$,因为不知道地球半径,故B错误;
C、已知地球绕太阳运行的周${T}_{2}^{\;}$及地球到太阳中心的距离${R}_{2}^{\;}$,只能计算中心天体太阳的质量,故C错误;
D、月球绕地球做圆周运动,地球对月球的万有引力提供圆周运动的向心力$G\frac{Mm}{({R}_{1}^{\;}+{R}_{地}^{\;})_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{1}^{2}}({R}_{1}^{\;}+{R}_{地}^{\;})$,可得地球质量$M=\frac{4{π}_{\;}^{2}({R}_{1}^{\;}+{R}_{地}^{\;})_{\;}^{3}}{G{T}_{1}^{2}}$,因为不知道地球半径,故D错误
故选:A
点评 万有引力提供向心力,根据数据列式可求解中心天体的质量,注意向心力的表达式需跟已知量相一致,同时注意隐形条件的挖掘,例如本题中的同步卫星的周期.

| A. | 相撞后某些速度增大的碎片,要靠近地球运动 | |
| B. | 相撞后某些速度增大的碎片,要远离地球运动 | |
| C. | 相撞后所有的碎片都要靠近地球运动 | |
| D. | 相撞后所有的碎片都要远离地球运动 |
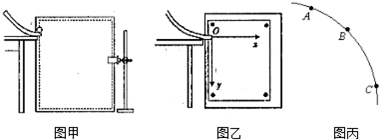
(1)若用20分度的游标卡尺测得遮光片的宽度b,如图乙所示,则b=9.50mm.
(2)若用d表示A点到导轨底端C点的距离,h表示A与C的高度差,b表示遮光片的宽度,在误差范围内,若公式$\frac{{b}^{2}}{{t}^{2}}=\frac{2gsh}{d}$成立,就可以验证机械能守恒定律(用题中给出的物理量符号表示).
(3)多次改变光电门的位置,每次均令滑块自A点静止释放下滑,测量相应的s与t值,结果如下表所示:
| 1 | 2 | 3 | 4 | 5 | |
| s(m) | 0.600 | 0.800 | 1.000 | 1.200 | 1.400 |
| t(ms) | 8.22 | 7.12 | 6.00 | 5.81 | 5.38 |
| $\frac{1}{{t}^{2}}$(102s-2) | 1.48 | 1.97 | 2.78 | 2.96 | 3.45 |

| A. | $\frac{1}{2}$ma2t2 | B. | $\frac{1}{2}$mgat2 | C. | $\frac{1}{2}$m(g+a)at2 | D. | $\frac{1}{2}$mg2t2 |
 如图所示,在火星与木星轨道之间有一小行星带.假设该带中的小行星只受到太阳的引力,并绕太阳做匀速圆周运动.下列说法中正确的是( )
如图所示,在火星与木星轨道之间有一小行星带.假设该带中的小行星只受到太阳的引力,并绕太阳做匀速圆周运动.下列说法中正确的是( )| A. | 各小行星绕太阳运动的周期小于一年 | |
| B. | 与太阳距离相等的每一颗小行星,受到太阳的引力大小都相等 | |
| C. | 小行星带内侧行星的加速度大于外侧行星的加速度 | |
| D. | 小行星带内各行星绕太阳公转的线速度均小于地球公转的线速度 |

(1)实验明使小车在砝码和托盘的牵引下运动,以此定量探究细绳拉力做功与小车动能变化的关系.
①实验准备了打点计时器及配套的电源、导线、复写纸及图1所示的器材.若要完成该实验,必需的实验器材还有刻度尺;天平(带砝码).
②为达到平衡摩擦力的目的,取下细绳和托盘,通过调节垫片的位置,改变长木板倾斜程度,根据打出的纸带判断小车是否做匀速直线运动运动.
③实验开始时,先调节木板上定滑轮的高度,使牵引小车的细绳与木板平行.这样做的目的是D(填字母代号).
A.避免小车在运动过程中发生抖动 B.可使打点计时器在纸带上打出的点迹清晰
C.可以保证小车最终能够实现匀速直线运动 D.可在平衡摩擦力后使细绳拉力等于小车受的合力
(2)连接细绳及托盘,放入砝码,通过实验得到图2所示的纸带.纸带上O为小车运动起始时刻所打的点,选取时间间隔为0.1s的相邻计数点A、B、C、D、E、F、G.实验时测得小车的质量为M=200g,小车所受细绳的拉力为F=0.2N.各计数点到O的距离为s,对应时刻小车的瞬时速度为v,小车所受拉力做的功为W,小车动能的变化为△Ek.请计算前补填表中空格(结果保留小数点后四位).
| 计数点 | s/m | v/(m•s-1) | v2/(m2•s-2) | W/J | △Ek/J |
| A | 0.1550 | 0.5560 | 0.3091 | 0.0310 | 0.0309 |
| B | 0.2160 | 0.6555 | 0.4297 | 0.0432 | 0.0430 |
| C | 0.2861 | 0.7550 | 0.5700 | 0.0572 | 0.0570 |
| D | 0.3670 | 0.8570 | 0.7344 | 0.0734 | 0.0734 |
| E | 0.4575 | 0.9525 | 0.9073 | ||
| F | 0.5575 | 1.051 | 1.105 | 0.1115 | 0.1105 |
| G | 0.6677 | 1.150 | 1.323 | 0.1335 | 0.1323 |
(3)这个小组在之前的一次实验中分析发现拉力做功总是要比小车动能增量明显大一些.这一情况可能是下列个些原因造成的C(填字母代号).
A.在接通电源的同时释放了小车 B.小车释放时离打点计时器太近
C.平衡摩擦力时长木板倾斜程度不够 D.平衡摩擦力时长木板倾斜程度过大
(4)实验小组进一步讨论认为可以通过绘制v2-s图线来分析实验数据.请根据表中各计数点的实验数据在图3中标出对应的坐标点,并画出v2-s图线.分析△v2-s图线为一条通过原点的直线,直线的斜率如果在实验误差允许的范围内等于理论值,也可以得出相同的结论.这种方案中直线斜率表达式为k=$\frac{2F}{M}$(用题目中相关物理量字母表示).