题目内容
20. 如图所示,将一质量为m的小球从空中A点以水平速度v0抛出,经过一段时间后,小球经过B点,此过程中,小球的动能变化△EK=$\frac{3}{2}$mv02,不计空气阻力,则小球从A到B( )
如图所示,将一质量为m的小球从空中A点以水平速度v0抛出,经过一段时间后,小球经过B点,此过程中,小球的动能变化△EK=$\frac{3}{2}$mv02,不计空气阻力,则小球从A到B( )| A. | 下落高度为$\frac{3{v}_{0}^{2}}{2g}$ | B. | 速度增量为v0,方向竖直向下 | ||
| C. | 运动方向改变的角为60° | D. | 经过的时间为$\frac{2{v}_{0}}{g}$ |
分析 根据动能定理即可求解下落高度;
根据竖直方向是自由落体运动的位移与时间关系即可求解时间,根据加速度的定义可知△v=g△t,从而可解速度的增量;
求出竖直方向的速度,由三角函数知识可求解速度方向改变的夹角.
解答 解:A.从A到B过程,由动能定理可得:mgh=△EK=$\frac{3}{2}$mv02,解得:h=$\frac{3{v}_{0}^{2}}{2g}$,故A正确;
BD.由h=$\frac{1}{2}$gt2得,下落时间t=$\sqrt{\frac{2h}{g}}$=$\frac{\sqrt{3}{v}_{0}}{g}$,速度增量为△v=g△t=g×$\frac{\sqrt{3}{v}_{0}}{g}$=$\sqrt{3}$v0,方向竖直向下,故BD错误;
C.设速度方向改变的夹角为α,则:tanα=$\frac{gt}{{v}_{0}}$=$\frac{\sqrt{3}{v}_{0}}{{v}_{0}}$=$\sqrt{3}$,所以速度方向改变的夹角为α=600,故C正确.
故选:AC.
点评 解答此题应明确:①当不涉及方向、时间的有关问题应用动能定理求解较方便;②求速度变化量时,应用△v=a△t求解较方便.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
14. -质量为m的实心均匀、横截面积为等边三角形的物体,沿两斜边的中点连线分别为A、B两部分,放置在光滑的支架上,支架间的距离为三角形边长的$\frac{1}{3}$,如图(a)所示;同样的等边三角形物体沿角平分线分割成C、D两部分,放置在间距为三角形边长$\frac{1}{2}$的光滑支架上,如图(b)所示,两物体均处于静止状态,则下列说法正确的是( )
-质量为m的实心均匀、横截面积为等边三角形的物体,沿两斜边的中点连线分别为A、B两部分,放置在光滑的支架上,支架间的距离为三角形边长的$\frac{1}{3}$,如图(a)所示;同样的等边三角形物体沿角平分线分割成C、D两部分,放置在间距为三角形边长$\frac{1}{2}$的光滑支架上,如图(b)所示,两物体均处于静止状态,则下列说法正确的是( )
 -质量为m的实心均匀、横截面积为等边三角形的物体,沿两斜边的中点连线分别为A、B两部分,放置在光滑的支架上,支架间的距离为三角形边长的$\frac{1}{3}$,如图(a)所示;同样的等边三角形物体沿角平分线分割成C、D两部分,放置在间距为三角形边长$\frac{1}{2}$的光滑支架上,如图(b)所示,两物体均处于静止状态,则下列说法正确的是( )
-质量为m的实心均匀、横截面积为等边三角形的物体,沿两斜边的中点连线分别为A、B两部分,放置在光滑的支架上,支架间的距离为三角形边长的$\frac{1}{3}$,如图(a)所示;同样的等边三角形物体沿角平分线分割成C、D两部分,放置在间距为三角形边长$\frac{1}{2}$的光滑支架上,如图(b)所示,两物体均处于静止状态,则下列说法正确的是( )| A. | 两种情况下支架对物体的作用力相等 | |
| B. | A部分对B部分的作用力等于$\frac{1}{2}$mg | |
| C. | 支架对C部分的作用力等于mg | |
| D. | A、B两部分之间和C、D两部分之间都没有摩擦力 |
8. 沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则下列选项正确的是( )
沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则下列选项正确的是( )
 沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则下列选项正确的是( )
沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则下列选项正确的是( )| A. | Ta=Tb=Td=Tc,Ea>Eb=Ed>Ec | |
| B. | Ta=Tb=Td=Tc,Ea=Eb=Ed=Ec | |
| C. | 此过程中棱台对从a点运动的小球做正功 | |
| D. | 此过程中棱台对从d点运动的小球做正功 |
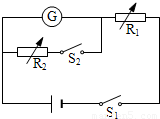 在把一个2mA电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材:
在把一个2mA电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材: 如图所示,在有活塞的气缸中密闭着一定质量的理想气体,将一个半导体热敏电阻(阻值随温度的升高而减小)R置于气缸中,气缸固定不动,缸内活塞可以自由移动且不漏气,活塞下挂一沙桶,沙桶装满沙子时活塞恰好能够静止.热敏电阻R与汽缸外的电源E和灵敏电流表A组成闭合回路,气缸和活塞具有良好的绝热性能.如果在沙桶的底部钻上一个小孔,那么在细沙缓缓漏出的过程中,以下判断正确的是( )
如图所示,在有活塞的气缸中密闭着一定质量的理想气体,将一个半导体热敏电阻(阻值随温度的升高而减小)R置于气缸中,气缸固定不动,缸内活塞可以自由移动且不漏气,活塞下挂一沙桶,沙桶装满沙子时活塞恰好能够静止.热敏电阻R与汽缸外的电源E和灵敏电流表A组成闭合回路,气缸和活塞具有良好的绝热性能.如果在沙桶的底部钻上一个小孔,那么在细沙缓缓漏出的过程中,以下判断正确的是( ) 如图所示,半径R=0.1m的竖直半圆形光滑轨道BC与水平面AB相切,AB距离x=1m.质量m=0.1kg的小滑块1放在半圆形轨道末端的B点,另一质量也为m=0.1kg的小滑块2,从A点以v0=2$\sqrt{10}$m/s的初速度在水平面上滑行,两滑块相碰,碰撞时间极短,碰后两滑块粘在一起滑上半圆形轨道.已知滑块2与水平面之间的动摩擦因数μ=0.2.取重力加速度g=10m/s2.两滑块均可视为质点.求:
如图所示,半径R=0.1m的竖直半圆形光滑轨道BC与水平面AB相切,AB距离x=1m.质量m=0.1kg的小滑块1放在半圆形轨道末端的B点,另一质量也为m=0.1kg的小滑块2,从A点以v0=2$\sqrt{10}$m/s的初速度在水平面上滑行,两滑块相碰,碰撞时间极短,碰后两滑块粘在一起滑上半圆形轨道.已知滑块2与水平面之间的动摩擦因数μ=0.2.取重力加速度g=10m/s2.两滑块均可视为质点.求: