题目内容
20.图甲所示是游乐场中过山车的实物图片,图乙是由它抽象出来的理想化模型(圆形轨道与斜轨道之间平滑连接,不计摩擦和空气阻力).已知圆轨道的半径为R,质量为m的小车(视作质点)从P点由静止沿斜轨道下滑,进入圆轨道后沿圆轨道运动.已知P点到圆轨道最低点B的高度差H=3R,求: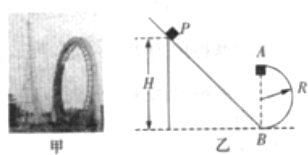
(1)小车到达B点时的速度大小;
(2)小车在A点受到的压力大小.
分析 (1)不计摩擦和空气阻力,小车下滑的过程中机械能守恒,由机械能守恒定律求出小车到达B点时的速度大小.
(2)研究P到A的过程,运用机械能守恒定律求出小车到达A点时的速度,在A点,由合力提供小车需要的向心力,由牛顿第二定律求解即可.
解答 解:(1)设小车滑至B点的速度为vB,根据机械能守恒定律得
mgH=$\frac{1}{2}m{v}_{B}^{2}$
又 H=3R
解得 vB=$\sqrt{6gR}$
(2)设小车从P点滑至A点的速度为vA,根据机械能守恒定律得
mgH=$\frac{1}{2}m{v}_{A}^{2}$+mg•2R
设小车在A点受到的压力大小为F,根据牛顿第二定律得
F+mg=m$\frac{{v}_{A}^{2}}{R}$
解得 F=mg
答:
(1)小车到达B点时的速度大小是$\sqrt{6gR}$;
(2)小车在A点受到的压力大小是mg.
点评 本题关键根据机械能守恒定律求解速度,根据牛顿第二定律和圆周运动的规律求解力.要知道圆周运动所需要的向心力是由指向圆心的合力提供的.

练习册系列答案
相关题目
5.放射性元素A经过2次α衰变和1次β衰变后生成一新元素B,则元素B在元素周期表中的位置较元素A的位置向前移动了( )
| A. | 1位 | B. | 2位 | C. | 3位 | D. | 4位 |
15. 如图所示,线圈L的自感系数足够大,直流电阻为零,两灯D1、D2的阻值相同.下列说法中正确的是( )
如图所示,线圈L的自感系数足够大,直流电阻为零,两灯D1、D2的阻值相同.下列说法中正确的是( )
 如图所示,线圈L的自感系数足够大,直流电阻为零,两灯D1、D2的阻值相同.下列说法中正确的是( )
如图所示,线圈L的自感系数足够大,直流电阻为零,两灯D1、D2的阻值相同.下列说法中正确的是( )| A. | K闭合的瞬间,D1和D2 一样亮 | |
| B. | K闭合的瞬间,D1较亮,D2较暗 | |
| C. | 电路稳定后,D2发光,D1不亮 | |
| D. | K断开的瞬间,D2立即熄灭,D1亮一下后熄灭 |

 水平地面上放着如图所示的玻璃砖,横截面左半部分OAB为一半径为R的$\frac{1}{4}$圆,右半部分OBC为一直角三角形,角C等于30°,玻璃砖折射率n=$\sqrt{3}$.现有一知入射光线如图所示平行于地面射到玻璃砖AB面上,已知入射光线与地面的距离为H=$\frac{\sqrt{3}R}{2}$,光在真空中的速度为c.求:
水平地面上放着如图所示的玻璃砖,横截面左半部分OAB为一半径为R的$\frac{1}{4}$圆,右半部分OBC为一直角三角形,角C等于30°,玻璃砖折射率n=$\sqrt{3}$.现有一知入射光线如图所示平行于地面射到玻璃砖AB面上,已知入射光线与地面的距离为H=$\frac{\sqrt{3}R}{2}$,光在真空中的速度为c.求: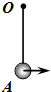 如图所示,一根长为L=0.2m的刚性轻绳,一端固定在O点,另一端连接一个质量为m的小球,当球自由悬挂时,球处在最低点A点,此时给球一个水平初速度v0让它运动起来,忽略空气阻力,重力加速度g=10m/s2
如图所示,一根长为L=0.2m的刚性轻绳,一端固定在O点,另一端连接一个质量为m的小球,当球自由悬挂时,球处在最低点A点,此时给球一个水平初速度v0让它运动起来,忽略空气阻力,重力加速度g=10m/s2 一边长为l的正方体玻璃砖,其切面如图.一束光从AD中点E射入,与AD夹角为45°时,折射光线恰好在AB面F点(图中没有画出)发生全反射,求该玻璃砖的折射率及F离B点距离.
一边长为l的正方体玻璃砖,其切面如图.一束光从AD中点E射入,与AD夹角为45°时,折射光线恰好在AB面F点(图中没有画出)发生全反射,求该玻璃砖的折射率及F离B点距离. 如图,A、C两点分别位于x轴和y轴上,∠OCA=30°,OA的长度为L.在△OCA区域内有垂直于xOy平面向里的匀强磁场.质量为m、电荷量为q的带正电粒子,以平行于y轴的方向从OA边射入磁场.已知粒子从某点射入时,恰好垂直于OC边射出磁场,且粒子在磁场中运动的时间为t0.不计重力.
如图,A、C两点分别位于x轴和y轴上,∠OCA=30°,OA的长度为L.在△OCA区域内有垂直于xOy平面向里的匀强磁场.质量为m、电荷量为q的带正电粒子,以平行于y轴的方向从OA边射入磁场.已知粒子从某点射入时,恰好垂直于OC边射出磁场,且粒子在磁场中运动的时间为t0.不计重力.