题目内容
如图所示,a、b 两小球在竖直光滑圆轨道内侧水平直径的左端 C,以足够大的相等的速率v 沿竖直方向反方向射出.当两球运动到某点重新相遇时的速率分别为 va 和 vb,若不计空气阻力,则( )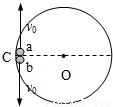
A.va<v b<v
B.va>v b>v
C.va=v b<v
D.va=v b>v
【答案】分析:如图,a球上升会减速,b球下降会加速,故a球的平均速率较小,两球应在CO连线上方相遇,根据机械能守恒定律得到相遇时速度大小关系.
解答: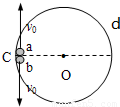 解:如图,a球上升过程会减速,b球下降会加速,故a球的平均速率较小,可能在d方相遇;
解:如图,a球上升过程会减速,b球下降会加速,故a球的平均速率较小,可能在d方相遇;
由于初速度相等,根据机械能守恒定律得 mghd+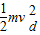 =
=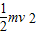
得:vd=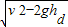
可见,相遇时va=vb<v.
故选C
点评:本题关键结合机械能守恒定律分析,明确上方小球先减速后加速,下方小球先加速后减速,故上方小球的平均速率小于初速度,下方小球的平均速度大于初速度.
解答:
 解:如图,a球上升过程会减速,b球下降会加速,故a球的平均速率较小,可能在d方相遇;
解:如图,a球上升过程会减速,b球下降会加速,故a球的平均速率较小,可能在d方相遇;由于初速度相等,根据机械能守恒定律得 mghd+
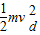 =
=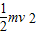
得:vd=
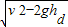
可见,相遇时va=vb<v.
故选C
点评:本题关键结合机械能守恒定律分析,明确上方小球先减速后加速,下方小球先加速后减速,故上方小球的平均速率小于初速度,下方小球的平均速度大于初速度.

练习册系列答案
相关题目
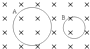 如图所示,A、B两个闭合线圈用同样的导线制成,匝数均为10匝,半径RA=2RB,图示区域内有磁感应强度均匀减小的匀强磁场,则A、B线圈中( )
如图所示,A、B两个闭合线圈用同样的导线制成,匝数均为10匝,半径RA=2RB,图示区域内有磁感应强度均匀减小的匀强磁场,则A、B线圈中( )| A、产生的感应电动势之比2:1 | B、产生的感应电动势之比4:1 | C、产生的感应电流之比2:1 | D、产生的感应电流之比4:1 |
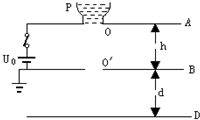 三块相同的金属平板A、B、D自上而下水平放置,间距分别为h和d,如图所示.A、B两板中心开孔,在A板的开孔上搁有一金属容器P,与A板接触良好,其内盛有导电液体.A板通过闭合的电键K与电动势为U0的电池正极相连,B板与电池负极相连并接地.容器P内液体在底部小孔O处形成质量为m,带电量为q的液滴后自由下落,穿过B板的开孔O′落到D板上,其电荷被D板吸附,液体随即蒸发.接着容器底部又形成相同的液滴自由下落,如此继续.设整个装置放在真空中.
三块相同的金属平板A、B、D自上而下水平放置,间距分别为h和d,如图所示.A、B两板中心开孔,在A板的开孔上搁有一金属容器P,与A板接触良好,其内盛有导电液体.A板通过闭合的电键K与电动势为U0的电池正极相连,B板与电池负极相连并接地.容器P内液体在底部小孔O处形成质量为m,带电量为q的液滴后自由下落,穿过B板的开孔O′落到D板上,其电荷被D板吸附,液体随即蒸发.接着容器底部又形成相同的液滴自由下落,如此继续.设整个装置放在真空中.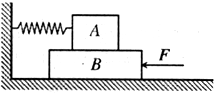 如图所示,A、B两物体叠放在水平地面上,A与B之间M、B与地面之间的动摩擦因数均为0.50,A物体质量m=30kg,B物体质量为l0kg.处于水平位置的轻弹簧一端固定于墙壁,另一端与A物体相连,弹簧处于自然状态,其劲度系数为250N/m.现有一水平推力F作用于物体B上,使B缓慢地向墙壁移动,当移动到某处时,A、B间开始发生相对滑动,此时水平推力F的大小为
如图所示,A、B两物体叠放在水平地面上,A与B之间M、B与地面之间的动摩擦因数均为0.50,A物体质量m=30kg,B物体质量为l0kg.处于水平位置的轻弹簧一端固定于墙壁,另一端与A物体相连,弹簧处于自然状态,其劲度系数为250N/m.现有一水平推力F作用于物体B上,使B缓慢地向墙壁移动,当移动到某处时,A、B间开始发生相对滑动,此时水平推力F的大小为 如图所示,A、B两小球用轻杆连接,竖直放置.由于微小的扰动,A球沿竖直光滑槽运动,B球沿水平光滑槽运动.则在A球到达底端前( )
如图所示,A、B两小球用轻杆连接,竖直放置.由于微小的扰动,A球沿竖直光滑槽运动,B球沿水平光滑槽运动.则在A球到达底端前( ) (2010?南昌一模)如图所示,A,B两木块质量分别为4kg和1kg,C板的质量为5kg,A、C之间的动摩擦因数为0.25,桌面光滑,A、C静止时,将木块B由张紧状态抬高0.8m后释放,滑轮的摩擦、绳的质量和伸长都不计,绳子足够牢固,问:
(2010?南昌一模)如图所示,A,B两木块质量分别为4kg和1kg,C板的质量为5kg,A、C之间的动摩擦因数为0.25,桌面光滑,A、C静止时,将木块B由张紧状态抬高0.8m后释放,滑轮的摩擦、绳的质量和伸长都不计,绳子足够牢固,问: