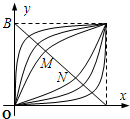
 幂函数y=xα,当α取不同的正数时,在区间[0,1]上它们的图象是一族美丽的曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图象三等分,即有BM=MN=NA.那么,αβ=( )
幂函数y=xα,当α取不同的正数时,在区间[0,1]上它们的图象是一族美丽的曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图象三等分,即有BM=MN=NA.那么,αβ=( )| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
 幂函数y=xα,当α取不同的正数时,在区间[0,1]上它们的图象是一族美丽的曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图象三等分,即有BM=MN=NA.那么,αβ=( )
幂函数y=xα,当α取不同的正数时,在区间[0,1]上它们的图象是一族美丽的曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图象三等分,即有BM=MN=NA.那么,αβ=( )| A、1 | ||
| B、2 | ||
C、
| ||
D、
|