在各棱长都相等的三棱锥A-BCD中，二面角A-BC-D的余弦值等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
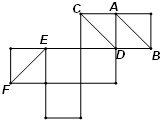如图是一个正方体纸展开图，如果将它还原成正方体，那么直线AB，CD，EF在原正方体的位置关系是（ ）| A、AB∥CD，EF⊥CD |
| B、AB与CD异面成角60°，CD与EF相交成角60° |
| C、AB∥CD，CD与EF相交成角60° |
| D、EF⊥CD，AB与CD异面成角60° |
若在三角形ABC中，已知a2=b2+c2+bc，则角A为（ ）
| A、60° | B、120° |
| C、30° | D、60°或120° |
将正方形ABCD沿对角线BD折起，使平面ABD⊥平面CBD，E是CD的中点，则AE与平面ABD所成角的正弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知复数z满足（2-i）z=4+3i（i为虚数单位），则|z-i|=（ ）
A、
| ||
B、
| ||
C、2
| ||
D、2
|
已知集合A={0，1，2，3}，B={x|x2-x=0}，则集合A∩B=（ ）
| A、{0} | B、{1，2，3} |
| C、{0，1} | D、{1} |
cos（-1560°）的值为（ ）
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知双曲线
-
=1(b＞a＞0)的两条渐近线为l1，l2，过右焦点F作垂直l1的直线交l1，l2于A，B两点．若|OA|，|AB|，|OB|成等差数列，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
平面内有n个圆，其中每两个圆都相交于两点，且每三个圆都不共点，用f（n）表示这n个圆把平面分割的区域数，那么f（n+1）与f（n）之间的关系为（ ）
| A、f（n+1）=f（n）+n |
| B、f（n+1）=f（n）+2n |
| C、f（n+1）=f（n）+n+1 |
| D、f（n+1）=f（n）+n-1 |