复数 ( )
( )
| A.i | B. | C.1 | D. |
已知 ,其中
,其中 是实数,i是虚数单位,则
是实数,i是虚数单位,则 i
i
A. i i | B. i i | C. i i | D. i i |
设复数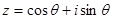 ,
,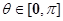 ,
,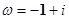 ,则
,则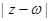 的最大值是( )
的最大值是( )
A.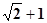 | B.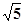 | C.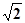 | D.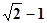 |
观察等式


由此得出以下推广命题不正确的是
A. |
B. |
C. |
D. |
下面给出了关于复数的四种类比推理:
①复数的加减法运算可以类比多项式的加减法运算法则;
②由向量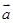 的性质
的性质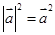 类比得到复数
类比得到复数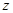 的性质
的性质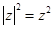 ;
;
③方程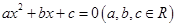 有两个不同实数根的条件是
有两个不同实数根的条件是 可以类比得到:方程
可以类比得到:方程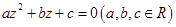 有两个不同复数根的条件是
有两个不同复数根的条件是 ;
;
④由向量加法的几何意义可以类比得到复数加法的几何意义
其中类比得到的结论错误的是
| A.①③ | B.②④ | C.②③ | D.①④ |
复数 的值为
的值为
A. | B. | C. | D. |
计算 的结果是
的结果是
A. | B. | C. | D. |
复数z= (1+
(1+ )在复平面上对应的点位于
)在复平面上对应的点位于
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
在复平面内,复数 对应的点在( )
对应的点在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
i(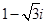 )=( )
)=( )
A.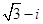 | B.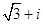 | C. | D. |