题目内容
9.已知定点M(2,0),若过点M的直线l(斜率不为零)与椭圆$\frac{{x}^{2}}{3}$+y2=1交于不同的两点E,F(E在点M,F之间),记λ=$\frac{{S}_{△OME}}{{S}_{△OMF}}$,求λ的取值范围.分析 如图所示,设E(x1,y1),F(x2,y2).(不妨设y1,y2>0).直线l的方程为:my+2=x.与椭圆方程联立化为:(m2+3)y2+4my+1=0,△>0,λ=$\frac{{S}_{△OME}}{{S}_{△OMF}}$=$\frac{|ME|}{|MF|}$=$\frac{{y}_{1}}{{y}_{2}}$<1,利用$\frac{({y}_{1}+{y}_{2})^{2}}{{y}_{1}{y}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$+2+$\frac{{y}_{2}}{{y}_{1}}$=λ+2+$\frac{1}{λ}$,进而得出.
解答 解:如图所示,
设E(x1,y1),F(x2,y2).(不妨设y1,y2>0).
直线l的方程为:my+2=x.
联立$\left\{\begin{array}{l}{my+2=x}\\{{x}^{2}+3{y}^{2}=3}\end{array}\right.$,化为:(m2+3)y2+4my+1=0,
△=16m2-4(m2+3)=12m2-12>0,解得m>1或m<-1.
∴y1+y2=-$\frac{4m}{{m}^{2}+3}$,y1•y2=$\frac{1}{{m}^{2}+3}$,
设原点O到直线l的距离为d.
∴λ=$\frac{{S}_{△OME}}{{S}_{△OMF}}$=$\frac{\frac{1}{2}d|ME|}{\frac{1}{2}d|MF|}$=$\frac{|ME|}{|MF|}$=$\frac{{y}_{1}}{{y}_{2}}$<1,
∴$\frac{({y}_{1}+{y}_{2})^{2}}{{y}_{1}{y}_{2}}$=$\frac{(-\frac{4m}{{m}^{2}+3})^{2}}{\frac{1}{{m}^{2}+3}}$=$\frac{16{m}^{2}}{{m}^{2}+3}$=$\frac{{y}_{1}}{{y}_{2}}$+2+$\frac{{y}_{2}}{{y}_{1}}$=λ+2+$\frac{1}{λ}$,
∵$\frac{16{m}^{2}}{{m}^{2}+3}$=$\frac{16}{1+\frac{3}{{m}^{2}}}$∈(4,16),
∴4<λ+2+$\frac{1}{λ}$<16,又λ<1,
解得:$7-4\sqrt{3}$<λ<1.
∴λ的取值范围是($7-4\sqrt{3}$,1).
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、不等式的解法与性质、三角形面积计算公式,考查了推理能力与计算能力,属于难题.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | (0,$\frac{1}{4}$] | B. | [$\frac{1}{4}$,1) | C. | (0,$\frac{1}{2}$] | D. | [$\frac{1}{4}$,$\frac{1}{2}$]∪(1,+∞) |
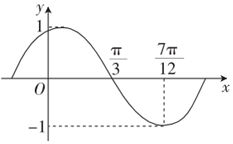 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),其部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),其部分图象如图所示.