题目内容
13.已知f(x)=ax2-2x+2,a∈R(1)已知h(10x)=f(x)+x+1,求h(x)的解析式;
(2)若f(x)>0在x∈[1,2]恒成立,求a的取值范围;
(3)设函数F(x)=|f(x)|,若对任意x1,x2∈[1,2],且x1≠x2,满足$\frac{{F({x_1})-F({x_2})}}{{{x_1}-{x_2}}}$>0,求实数a的取值范围.
分析 (1)令10x=t,得:x=lgt,从而求出h(x)的解析式即可;
(2)分离此时a,得到$a>-{(\frac{1}{x})^2}+\frac{2}{x},x∈[1,2]$恒成立,根据二次函数的性质求出a的范围即可;
(3)通过讨论a的范围求出F(x)的单调性,从而进一步确定a的范围即可.
解答 解:(1)令10x=t即x=lgt,由h(10x)=ax2-x+3得h(t)=alg2t-lgt+3
即h(x)=alg2x-lgx+3
(2)由题意得:ax2-2x+2>0即$a>-{(\frac{1}{x})^2}+\frac{2}{x},x∈[1,2]$恒成立,
$-{(\frac{1}{x})^2}+\frac{2}{x}=-2{(\frac{1}{x}-\frac{1}{2})^2}+\frac{1}{2}$,当x=2时${[-{(\frac{1}{x})^2}+\frac{2}{x}]_{max}}=\frac{1}{2}$,
所以a得取值范围为$a>\frac{1}{2}$
(3)由题意得F(x)=|f(x)|在x∈[1,2]单调递增,
①当a<0时,f(x)=ax2-2x+2,对称轴为$x=\frac{1}{a}<0$
又因为f(0)>0且f(x)在x∈[1,2]单调递减,且f(1)=a<0,
所以F(x)=|f(x)|在x∈[1,2]单调递增.
②当a=0时,f(x)=-2x+2,f(x)在x∈[1,2]单调递减,且f(1)=0,
所以F(x)=|f(x)|在x∈[1,2]单调递增;
③当$0<a≤\frac{1}{2}$时,f(x)=ax2-2x+2,对称轴为$x=\frac{1}{a}∈[2,+∞)$,
所以f(x)在x∈[1,2]单调递减,
要使F(x)=|f(x)|在x∈[1,2]单调递增.f(1)=a<0不符合,舍去;
④当$\frac{1}{2}<a<1$时,f(x)=ax2-2x+2,对称轴为$x=\frac{1}{a}∈(1,2)$,
可知F(x)=|f(x)|在x∈[1,2]不单调.
⑤当a≥1时,f(x)=ax2-2x+2,对称轴为$x=\frac{1}{a}∈(0,1]$
所以f(x)在x∈[1,2]单调递增,f(1)=a>0
要使F(x)=|f(x)|在x∈[1,2]单调递增.故a≥1;
综上所述,a的取值范围为(-∞,0]∪[1,+∞)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.

| A. | a>0且b>0 | B. | a>0或b>0 | C. | b≥0或b≥0 | D. | a≥0且b≥0 |
 在△ABC中,角A,B,C所对的边分别为a,b,c,已知${S_{△ABC}}=\frac{{\sqrt{3}}}{2}accosB$,
在△ABC中,角A,B,C所对的边分别为a,b,c,已知${S_{△ABC}}=\frac{{\sqrt{3}}}{2}accosB$,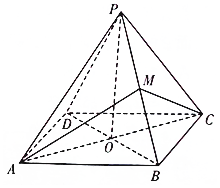 四棱锥P-ABCD的四条侧棱长相等,底面ABCD为正方形,M为PB的中点.
四棱锥P-ABCD的四条侧棱长相等,底面ABCD为正方形,M为PB的中点.