题目内容
若函数f(x)=xlnx的图象在x=1处的切线为l,则l上的点到圆x2+y2+4x-2y+4=0上的点的最近距离是( )
A、2
| ||
B、
| ||
C、2
| ||
| D、1 |
分析:先对函数进行求导,把x=1代入求得切线的斜率,进而利用切点求得切线的方程,整理圆的方程为标准方程求得圆心和半径,进而利用点到直线的距离求得圆心到切线的距离,减去半径的长即是l上的点到圆的最小距离.
解答:解:y'=1•lnx+x•
=lnx+1
x=1,y'=0+1=1
即切线斜率是1
x=1,y=1×0=0
∴切点为(1,0)
所以切线方程为x-y-1=0
整理圆的方程得(x+2)2+(y-1)2=1,故圆心为(-2,1),
∴圆心到切线的距离为
=2
则切线与圆的位置关系为相离,圆的半径为1,
∴l上的点到圆的点的最小距离为2
-1
故选C
| 1 |
| x |
x=1,y'=0+1=1
即切线斜率是1
x=1,y=1×0=0
∴切点为(1,0)
所以切线方程为x-y-1=0
整理圆的方程得(x+2)2+(y-1)2=1,故圆心为(-2,1),
∴圆心到切线的距离为
| |-2-1-1| | ||
|
| 2 |
则切线与圆的位置关系为相离,圆的半径为1,
∴l上的点到圆的点的最小距离为2
| 2 |
故选C
点评:本题主要考查了点到直线的距离公式的应用,直线与圆的位置关系,导函数求切线的问题.考查了学生综合基础知识的应用和数形结合思想的应用.

练习册系列答案
相关题目
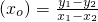 ,求证:xo>xl.
,求证:xo>xl.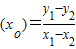 ,求证:xo>xl.
,求证:xo>xl.