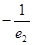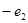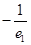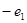题目内容
已知等比数列{am}的前m项和为Sm,若S =4(a1+a3+a5+…+a2m-1),a1a2a3=27,则a6=( )
=4(a1+a3+a5+…+a2m-1),a1a2a3=27,则a6=( )
| A.27 | B.81 | C.243 | D.729 |
C
解析试题分析:利用等比数列的性质可得a1a2a3=a2 =27,解得a2=3,因为S
=27,解得a2=3,因为S =4(a1+a3+a5+…+a2m-1),
=4(a1+a3+a5+…+a2m-1),
所以m=1时,则S2=a1+a2=4a1,从而可得 ,所以
,所以 =243,故选C.
=243,故选C.
考点:1.等比数列的性质;2.等比数列的通项公式.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
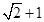 与
与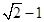 ,两数的等比中项是( )
,两数的等比中项是( )
A.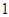 | B.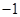 | C. | D.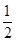 |
在正项等比数列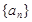 中,
中,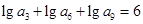 ,则
,则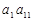 的值是( )
的值是( )
A.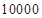 | B.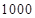 | C.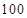 | D.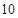 |
已知等比数列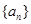 的公比
的公比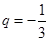 ,则
,则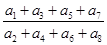 等于( )
等于( )
A. | B.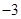 | C.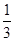 | D.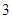 |
若公比为2且各项均为正数的等比数列 中,
中, ,则
,则 的值等于( )
的值等于( )
| A.2 | B.4 | C.8 | D.16 |
在正项等比数列{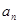 }中,
}中,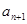 <
<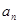 ,
,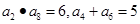 ,则
,则 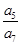 = ( )
= ( )
A.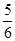 | B.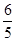 |
C.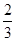 | D.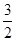 |
已知数列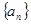 中,
中,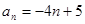 ,等比数列
,等比数列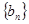 的公比
的公比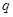 满足
满足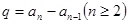 ,且
,且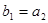 ,则
,则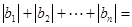
A.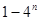 | B.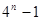 | C.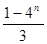 | D.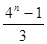 |
已知在等比数列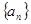 中,
中, ,
, ,那么
,那么 等于
等于
| A.5 | B.10 | C.15 | D.20 |
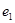 的椭圆与离心率为
的椭圆与离心率为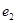 的双曲线有相同的焦点,且椭圆长轴的端点、短轴的端点、焦点到双曲线的一条渐近线的距离依次构成等比数列,则
的双曲线有相同的焦点,且椭圆长轴的端点、短轴的端点、焦点到双曲线的一条渐近线的距离依次构成等比数列,则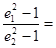 ( )
( )