题目内容
已知![]() ,在
,在![]() 与
与![]() 时,都取得极值.
时,都取得极值.
(1)求![]() 、b的值;
、b的值;
(2)若对![]() [一1,2],
[一1,2],![]() <c2恒成立,求c的取值范围.
<c2恒成立,求c的取值范围.
解:(1)由题设![]() 的两根为
的两根为![]() 和1,
和1,
由韦达定理,得 ,即
,即![]()
b=-2
(2)由(1)知![]() ,
,
且当![]() [一1,-
[一1,-![]() )时,
)时,![]() ;
;
![]() 时,
时,![]() ;
;
![]() 时,
时,![]()
所以当![]() 时,
时,![]() 有极大值
有极大值![]()
又![]() ,即当
,即当![]() 时,
时,![]() 有极大值为
有极大值为![]()
因为对![]() ,
,![]() <c2恒成立,所以c2>2+c,解得c<-1或c>2
<c2恒成立,所以c2>2+c,解得c<-1或c>2
故c的取值范围是(-![]() ,-1)(2,+
,-1)(2,+ ![]() )
)

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 在
在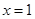 与
与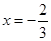 时,都取得极值.
时,都取得极值. 的值;
的值;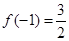 ,求
,求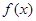 的单调区间和极值;
的单调区间和极值;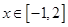 都有
都有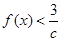 恒成立,求
恒成立,求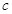 的取值范围.
的取值范围. ,在
,在 与
与 时,都取得极值。
时,都取得极值。 的值;
的值; 都有
都有 恒成立,求c的取值范围。
恒成立,求c的取值范围。 在
在 与
与 时,都取得极值。
时,都取得极值。 的值;
的值;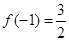 ,求
,求 的单调区间和极值;
的单调区间和极值; 都有
都有 恒成立,求
恒成立,求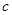 的取值范围。
的取值范围。 恒成立,求
恒成立,求 与函数
与函数