题目内容
10．函数f（x）=x2+$\frac{a}{x}$在区间（1，+∞）上是增函数，则实数a的最大值为（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
分析 求导数得到$f′（x）=\frac{2{x}^{3}-a}{{x}^{2}}$，由f（x）在区间（1，+∞）上是增函数便可得到a≤2x3在x∈（1，+∞）恒成立，而x＞1时，2x3＞2，这样即可得出a≤2，从而便可得出实数a的最大值．
解答 解：$f′（x）=2x-\frac{a}{{x}^{2}}=\frac{2{x}^{3}-a}{{x}^{2}}$；
f（x）在区间（1，+∞）上是增函数；
∴f′（x）≥0在x∈（1，+∞）上恒成立；
∴a≤2x3在x∈（1，+∞）上恒成立；
∵x∈（1，+∞）时，2x3＞2；
∴a≤2；
∴实数a的最大值为2．
故选D．
点评 考查函数单调性和函数导数符号的关系，由x＞1根据不等式的性质求2x3的范围，或根据函数y=2x3的单调性求2x3的范围．
练习册系列答案
相关题目
20．曲线y=x3-$\sqrt{3}x$+2上的任意一点P处切线的倾斜角的取值范围是（ ）
| A． | [$\frac{π}{3}$，$\frac{π}{2}$） | B． | [$\frac{2π}{3}$，π） | C． | [0，$\frac{π}{2}$）∪（$\frac{π}{2}$，$\frac{2π}{3}$] | D． | [0，$\frac{π}{2}$）∪[$\frac{2π}{3}$，π） |
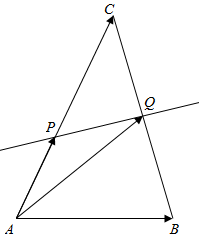如图，已知△ABC的边BC的垂直平分线交AC于点P，交BC于点Q，若|$\overrightarrow{AB}$|=3，|$\overrightarrow{AC}$|=5，则（$\overrightarrow{AP}$+$\overrightarrow{AQ}$）•（$\overrightarrow{AB}$-$\overrightarrow{AC}$）的值为-16．
20．已知f（x）=cosx•cos2x•cos4x，若f（α）=$\frac{1}{8}$，则角α不可能等于（ ）
| A． | $\frac{π}{9}$ | B． | $\frac{2π}{9}$ | C． | $\frac{2π}{7}$ | D． | $\frac{4π}{7}$ |