题目内容
O是△ABC的内切圆的圆心，|
|=5，|
|=4，|
|=3，则下列结论正确的是（ ）
| AB |
| BC |
| CA |
分析：由已知中△ABC的三边长，根据直角三角形内切圆半径公式，可求出△ABC的内切圆半径，进而根据勾股定理，可求出三个向量的模，进而得到答案．
解答：解：∵|
|=5，|
|=4，|
|=3，
∴△ABC的内切圆半径为
=1
在Rt△OCE中，OE=CE=1，
∴|
|=
=
在Rt△OBD中，OD=1，BD=4-1=3
∴|
|=
=
在Rt△OAE中，OE=1，AE=3-1=2
∴|
|=
=
故|
|＜|
|＜|
|
故选：A
| AB |
| BC |
| CA |
∴△ABC的内切圆半径为
| 4+3-5 |
| 2 |
在Rt△OCE中，OE=CE=1，
∴|
| OC |
| 12+12 |
| 2 |
在Rt△OBD中，OD=1，BD=4-1=3
∴|
| OB |
| 12+(4-1)2 |
| 10 |
在Rt△OAE中，OE=1，AE=3-1=2
∴|
| OA |
| 12+(3-1)2 |
| 5 |
故|
| OC |
| OA |
| OB |
故选：A
点评：本题考查的知识点是平面向量的应用，其中根据直角三角形内切圆半径公式，求出△ABC的内切圆半径，是解答的关键．
练习册系列答案
相关题目
设O是△ABC的内切圆的圆心，|
|=5，|
|=4，|
|=3，则下列结论正确的是（ ）
| AB |
| BC |
| CA |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
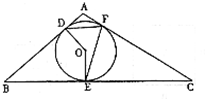如图，⊙O是△ABC的内切圆，切点分别是D、E、F，已知∠A=100°，∠C=30°，则∠DFE的度数是（ ）