题目内容
已知函数f(x)=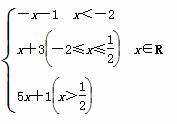 .
.
(1)求函数f(x)的最小值;
(2)已知m∈R,命题p:关于x的不等式f(x)≥m2+2m-2对任意m∈R恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
解析: (1)作出函数f(x)的图象,可知函数f(x)在(-∞,-2)上单调递减,在(-2,+∞)上单调递增,故f(x)的最小值为f(x)min=f(-2)=1.
(2)对于命题p,m2+2m-2≤1,故-3≤m≤1;
对于命题q,m2-1>1,故m> 或m<-
或m<- .
.
由于“p或q”为真,“p且q”为假,则
①若p真q假,则 解得-
解得- ≤m≤1.
≤m≤1.
②若p假q真,则 ,解得m<-3或m>
,解得m<-3或m> .
.
故实数m的取值范围是(-∞,-3)∪[- ,1]∪(
,1]∪( ,+∞).
,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
=3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )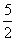 B.
B.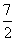
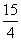 D.
D.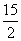
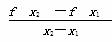 <0.如果f
<0.如果f =
=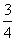 ,4f(log
,4f(log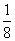 x)>3,那么x的取值范围为( )
x)>3,那么x的取值范围为( )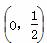 B.
B. 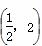
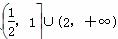 D.
D.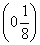 ∪
∪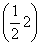

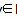 R,且|x+y|≤
R,且|x+y|≤ ,|x-y|≤
,|x-y|≤ ,求证:|x+5y|≤1.
,求证:|x+5y|≤1.