题目内容
若在△ABC中,角A,B,C所对的边分别为a,b,c若b2+c2-a2=bc,则A= .
分析:根据题中的等式,利用余弦定理算出cosA=
,结合0°<A<180°可得A=60°.
| 1 |
| 2 |
解答:解:∵在△ABC中,b2+c2-a2=bc,
∴根据余弦定理,得cosA=
=
=
又∵0°<A<180°,∴A=60°.
故答案为:60°
∴根据余弦定理,得cosA=
| b2+c2-a2 |
| 2bc |
| bc |
| 2bc |
| 1 |
| 2 |
又∵0°<A<180°,∴A=60°.
故答案为:60°
点评:本题给出三角形的三边的平方关系,求角A的大小.着重考查了利用余弦定理解三角形的知识,属于基础题.

练习册系列答案
相关题目
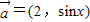 ,
,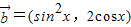 ,函数f(x)=
,函数f(x)=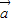 •
•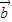 .
.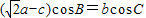 ,求f(A)的取值范围.
,求f(A)的取值范围.