题目内容
(2009天津卷文)(本小题满分14分)
已知椭圆![]() (
(![]() )的两个焦点分别为
)的两个焦点分别为![]() ,过点
,过点![]() 的直线与椭圆相交于点A,B两点,且
的直线与椭圆相交于点A,B两点,且![]()
(Ⅰ求椭圆的离心率
(Ⅱ)直线AB的斜率;
(Ⅲ)设点C与点A关于坐标原点对称,直线![]() 上有一点H(m,n)(
上有一点H(m,n)(![]() )在
)在![]() 的外接圆上,求
的外接圆上,求![]() 的值。
的值。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】 (1)解:由![]() ,得
,得![]() ,从而
,从而
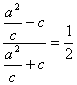 ,整理得
,整理得![]() ,故离心率
,故离心率![]()
(2)解:由(1)知,![]() ,所以椭圆的方程可以写为
,所以椭圆的方程可以写为![]()
设直线AB的方程为![]() 即
即![]()
由已知设![]() 则它们的坐标满足方程组
则它们的坐标满足方程组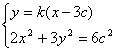
消去y整理,得![]()
依题意,![]()
而![]() ,有题设知,点B为线段AE的中点,所以
,有题设知,点B为线段AE的中点,所以![]()
联立三式,解得![]() ,将结果代入韦达定理中解得
,将结果代入韦达定理中解得![]()
(3)由(2)知,![]() ,当
,当![]() 时,得A
时,得A![]() 由已知得
由已知得![]()
线段![]() 的垂直平分线l的方程为
的垂直平分线l的方程为![]() 直线l与x轴的交点
直线l与x轴的交点![]() 是
是![]() 的外接圆的圆心,因此外接圆的方程为
的外接圆的圆心,因此外接圆的方程为![]()
直线![]() 的方程为
的方程为![]() ,于是点
,于是点![]() 满足方程组
满足方程组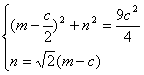 由
由![]() ,解得
,解得![]() ,故
,故![]()
当![]() 时,同理可得
时,同理可得![]()
【考点定位】本小题主要考查椭圆的标准方程和几何性质,直线方程,圆的方程等基础知识。考查用代数方法研究圆锥曲线的性质和数形结合的思想,考查运算能力和推理能力。

练习册系列答案
相关题目