题目内容
14.已知函数f(x)=|sinx|•cosx,则下列说法正确的是( )| A. | f(x)的图象关于直线x=$\frac{π}{2}$对称 | B. | f(x)在区间上[$\frac{π}{4}$,$\frac{3π}{4}$]单调递减 | ||
| C. | 若|f(x1)|=|f(x2)|,则x1=x2+2kπ(k∈Z) | D. | f(x)的周期为π |
分析 化简函数f(x),根据正弦函数的图象与性质,对选项中的命题进行分析、判断正误即可.
解答 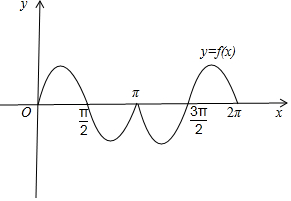 解:函数f(x)=|sinx|•cosx
解:函数f(x)=|sinx|•cosx
=$\left\{\begin{array}{l}{\frac{1}{2}sin2x,x∈[2kπ.2kπ+π]}\\{-\frac{1}{2}sin2x,x∈(2kπ-π,2kπ),k∈Z}\end{array}\right.$,
∴f(x)的图象关于直线x=kπ,k∈Z对称,A错误;
x∈[$\frac{π}{4}$,$\frac{3π}{4}$]时,2x∈[$\frac{π}{2}$,$\frac{3π}{2}$],f(x)是单调减函数,B正确;
|f(x1)|=|f(x2)|时,$\frac{{x}_{1}{+x}_{2}}{2}$=$\frac{π}{4}$+$\frac{kπ}{2}$,k∈Z,
∴x1+x2=$\frac{π}{2}$+kπ,k∈Z,
∴x1=$\frac{π}{2}$-x2+kπ,k∈Z,C错误;
画出函数f(x)的图象,如图所示,
∴f(x)的最小正周期为2π,∴D错误.
故选:B.
点评 本题考查了正弦函数的图象与性质的应用问题,也考查了命题真假的判断问题,是基础题.

练习册系列答案
相关题目
6.函数f(x)=x3-3x的单调递减区间为( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-1,1) | D. | (-∞,+∞) |
3.设$\overrightarrow a$,$\overrightarrow b$是两个不共线向量,且向量$\overrightarrow a+λ\overrightarrow b$与$-\overrightarrow b+2\overrightarrow a$共线,则λ=( )
| A. | 0 | B. | $-\frac{1}{2}$ | C. | -2 | D. | $\frac{1}{2}$ |
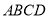 所在的平面与△
所在的平面与△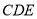 所在的平面交于
所在的平面交于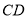 ,
,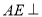 平面
平面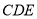 ,且
,且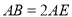 .
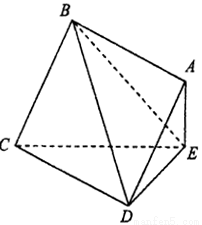
.
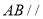 平面
平面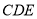 ;
;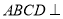 平面
平面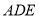 .
.