题目内容
按从小到大的顺序将20.6,(| 1 | 2 |
分析:由对数函数的图象和性质可得:log0.62<0,2<log26<3,再由指数函数的图象和性质可得:2>20.6>1,(
)6<(0.6)2<1
从而得到结果.
| 1 |
| 2 |
从而得到结果.
解答:解:由对数函数的图象和性质
可得:log0.62<0,2<log26<3
由指数函数的图象和性质
可得:2>20.6>1,(
)6<(0.6)2<1
∴log0.62<(
)6<(0.6)2<20.6<log26
故答案为:log0.62<(
)6<(0.6)2<20.6<log26
可得:log0.62<0,2<log26<3
由指数函数的图象和性质
可得:2>20.6>1,(
| 1 |
| 2 |
∴log0.62<(
| 1 |
| 2 |
故答案为:log0.62<(
| 1 |
| 2 |
点评:本题主要考查对数函数,指数函数的图象和性质,在比较大小中,一般是应用函数的单调性或函数图象的分布.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
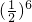 ,(0.6)2,log0.62,log26排成一排:________.
,(0.6)2,log0.62,log26排成一排:________. ,(0.6)2,log0.62,log26排成一排: .
,(0.6)2,log0.62,log26排成一排: .