题目内容
已知数列 的前
的前 项和
项和 ,满足
,满足 为常数,且
为常数,且 ,且
,且 是
是 与
与 的等差中项.
的等差中项.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(Ⅰ)
(Ⅱ)
【解析】
试题分析:应用项与和的关系,结合题中给的式子,构造出一个,两式相减,可得到数列的相邻两项之间的关系,从而得出数列为等比数列,在令n=1,求得对应的数列的首项,再结合题中的条件,可以求出参数的值,从而得出数列的通项公式,对于第二问,可以得出数列为等差和等比数列的对应项的积构成新数列求和用错位相减法.
试题解析:(Ⅰ)【解析】
(Ⅰ)  (1)
(1)
 (2)
(2)
 得:
得: 2分
2分
 为常数,
为常数, 成等比数列,
成等比数列, 为公比,
为公比,
当 时,
时, ,
, , 4分
, 4分
由题意可知: ,
,
 ,
, ,
, 或
或 (舍去) 6分
(舍去) 6分

 成等比数列,首项
成等比数列,首项 ,公比为
,公比为 ,
, . 7分
. 7分
(Ⅱ)
 (1) 8分
(1) 8分
 (2) 9分
(2) 9分
(1)-(2)得:


 11分
11分
 13分
13分
考点:数列的通项公式,和与项的关系,错位相减法求和.
考点分析: 考点1:等差数列 考点2:等比数列 考点3:数列的求和 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 的展开式中的常数项是
的展开式中的常数项是 B.
B. C.
C. D.
D.
 )的图像,可将函数
)的图像,可将函数 的图像向左平移m(m>0)个单位长度,则m的最小值是( )
的图像向左平移m(m>0)个单位长度,则m的最小值是( ) B.
B. D.
D.
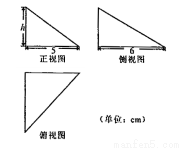
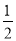
 中,若
中,若 ,则
,则 ;
; 中,
中, 成等比数列,则公比为
成等比数列,则公比为 ;
; ,则
,则 的最小值为
的最小值为 ;
; ,则
,则 .
.
 的焦距为
的焦距为 ,点
,点 在
在 的渐近线上,则
的渐近线上,则 的方程为( )
的方程为( )
 B.
B.


 D.
D.
 的棱长为
的棱长为 ,设
,设 ,则
,则 .
. 根据上述规律,第五个等式为__________________________.
根据上述规律,第五个等式为__________________________.