题目内容
已知sin（α-β）cosα-cos（β-α）sinα=
，β是第三象限角，求sinβ．
| 3 |
| 5 |
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：直接利用诱导公式化简已知条件，通过两角和的正弦函数求解即可．
解答：
解：sin（α-β）cosα-cos（β-α）sinα=
，
可得sin（α-β）cosα-cos（α-β）sinα=
，
可得sin（α-β-α）=
．
∴sinβ=-
．
| 3 |
| 5 |
可得sin（α-β）cosα-cos（α-β）sinα=
| 3 |
| 5 |
可得sin（α-β-α）=
| 3 |
| 5 |
∴sinβ=-
| 3 |
| 5 |
点评：本题考查诱导公式的应用，两角和的正弦函数的应用，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
抛物线y=4x2按照向量
=（1，2）平移后，其顶点在一次函数y=
x+
b的图象上，则b的值（ ）
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| A、2 | B、3 | C、4 | D、5 |
如果向量
=（1，2），
=（-2，0），那么
•
等于（ ）
| a |
| b |
| a |
| b |
| A、2 | B、-2 | C、1 | D、-1 |
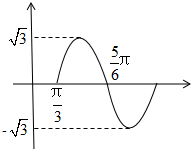已知函数y=Asin（ωx+φ）（A＞0，ω＞0），一个周期内的函数图象，如图所示，求：