题目内容
15.下列命题中,真命题的个数为( )①若a,b,c∈R则“a>b”是“ac2>bc2”成立的充分不必要条件;
②若椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1的两个焦点为F1,F2,且弦AB过点F1,则△ABF2的周长为20.
③若命题“¬p”与命题“p或q”都是真命题,则命题q一定是真命题;
④若命题p:?x∈R,x2+x+1<0,则¬p:?x∈R,x2+x+1≥0.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①当a=0时,“ac2=bc2”,充分性不成立,可判断①错误;
②由椭圆的方程$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1知长轴长为10,依题意,利用椭圆的定义可求得△ABF2的周长为20,可判断②正确;
③由命题“¬p”与命题“p或q”都是真命题,可知p假q真,可判断③正确;
④写出命题p的否定¬p:?x∈R,x2+x+1≥0,可判断④正确.
解答 解:对于①,若a,b,c∈R则“a>b”不能推出“ac2>bc2”,如c=0时就不成立,即充分性不成立,故①错误;
对于②,椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1的两个焦点为F1,F2,则长轴长为10,又弦AB过点F1,则△ABF2的周长l=|AB|+|AF2|+|BF2|=|AF1|+|BF1|+|AF2|+|BF2|=4a=20,故②正确;
对于③,若命题“¬p”与命题“p或q”都是真命题,则命题q一定是真命题,故③正确;
对于④,若命题p:?x∈R,x2+x+1<0,则¬p:?x∈R,x2+x+1≥0,故④正确.
综上所述,真命题的有个数为3个,
故选:C.
点评 本题考查命题的真假判断与应用,着重考查全称命题与特称命题的转化、充分必要条件的判断、命题及其否定及椭圆的定义的应用,属于基础题.

练习册系列答案
相关题目
4.已知向量$\overrightarrow a$,$\overrightarrow b$满足$|{\overrightarrow a}|=1$,($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,$({2\overrightarrow a+\overrightarrow b})⊥\overrightarrow b$,则向量$\overrightarrow a$,$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{3π}{4}$ |
6.已知函数f(x)=-x2+6x+a2-1,那么下列式子中正确的是( )
| A. | $f(\sqrt{2})<f(3)<f(4)$ | B. | $f(3)<f(\sqrt{2})<f(4)$ | C. | $f(\sqrt{2})<f(4)<f(3)$ | D. | $f(3)<f(4)<f(\sqrt{2})$ |
3.已知m∈R,i为虚数单位,若$\frac{m+i}{1-2i}$∈R,则实数m的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
7.log39=( )
| A. | 5 | B. | 2 | C. | 3 | D. | 4 |
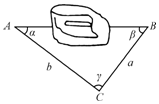 如图,某人为了测量某建筑物两侧A.B间的距离(在A,B处相互看不到对方),选定了一个可看到A、B两点的C点进行测量,你认为测量时应测量的数据是a,b,γ.
如图,某人为了测量某建筑物两侧A.B间的距离(在A,B处相互看不到对方),选定了一个可看到A、B两点的C点进行测量,你认为测量时应测量的数据是a,b,γ.