题目内容
2.已知在空间四边形OABC中,$\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\overrightarrow b,\overrightarrow{OC}=\overrightarrow c$,点M在OA上,且OM=3MA,N为BC中点,用$\overrightarrow a,\overrightarrow b,\overrightarrow c$表示$\overrightarrow{MN}$,则$\overrightarrow{MN}$等于-$\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$.分析 根据题意画出图形,结合图形,利用空间向量的线性运算法则,用$\overrightarrow{OA}$、$\overrightarrow{OB}$和$\overrightarrow{OC}$表示出$\overrightarrow{MN}$即可.
解答 解:如图所示,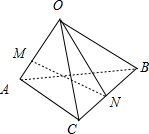
空间四边形OABC中,$\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\overrightarrow b,\overrightarrow{OC}=\overrightarrow c$,
∵点M在OA上,且OM=3MA,
∴$\overrightarrow{OM}$=$\frac{3}{4}$$\overrightarrow{OA}$;
又N为BC中点,
∴$\overrightarrow{ON}$=$\frac{1}{2}$($\overrightarrow{OB}$+$\overrightarrow{OC}$)
∴$\overrightarrow{MN}$=$\overrightarrow{ON}$-$\overrightarrow{OM}$
=$\frac{1}{2}$($\overrightarrow{OB}$+$\overrightarrow{OC}$)-$\frac{3}{4}$$\overrightarrow{OA}$
=-$\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$.
故答案为:$-\frac{3}{4}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$.
点评 本题考查了空间向量的线性表示与运算问题,是基础题.

| A. | a<c<b | B. | a<b<c | C. | b<c<a | D. | b<a<c |
| 付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
| 频数 | 20 | 20 | a | b |
(2)按分层抽样的方式从这100位顾客中抽出5人,再从抽出的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量η,求η的分布列及数学期望E(η).
| A. | ?x0≥0且x0∈R,${2^{x_0}}>{x_0}^2$ | B. | ?x≥0且x∈R,2x≤x2 | ||
| C. | ?x0≥0且x0∈R,${2^{x_0}}≤{x_0}^2$ | D. | ?x0<0且x0∈R,${2^{x_0}}≤{x_0}^2$ |
| A. | (-3,-2) | B. | (-3,2) | C. | (2,4) | D. | (-2,4) |
| A. | $\frac{16}{17}$ | B. | $\frac{36}{5}$ | C. | $\frac{64}{37}$ | D. | $\frac{196}{53}$ |