1. 图中三角形的总个数为 (
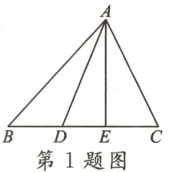
A.4
B.5
C.6
D.7
C
)
A.4
B.5
C.6
D.7
答案:C
解析:
以A为顶点,分别以BC上的线段为底边计数。BC上有BD、BE、BC、DE、DC、EC共6条线段,对应6个三角形:△ABD、△ABE、△ABC、△ADE、△ADC、△AEC。
2. 三角形按边分类可分为 (
A.不等边三角形、等边三角形
B.等腰三角形、等边三角形
C.不等边三角形、等腰三角形、等边三角形
D.不等边三角形、等腰三角形
D
)A.不等边三角形、等边三角形
B.等腰三角形、等边三角形
C.不等边三角形、等腰三角形、等边三角形
D.不等边三角形、等腰三角形
答案:D
解析:
三角形按边分类,三条边都不相等的三角形是不等边三角形;有两条边相等的三角形是等腰三角形。等边三角形是特殊的等腰三角形,即三条边都相等的等腰三角形,不应单独列为一类。因此,正确分类为不等边三角形和等腰三角形。
3. 已知三角形的三边长分别为$2$,$9$,$x$,若$x$为整数,则这样的三角形个数为 (
A.1
B.2
C.3
D.4
C
)A.1
B.2
C.3
D.4
答案:C
解析:
根据三角形三边关系,两边之和大于第三边,两边之差小于第三边。可得:$9 - 2 < x < 9 + 2$,即$7 < x < 11$。因为$x$为整数,所以$x$的值为$8$,$9$,$10$,共$3$个。
4. 如图,$AD$,$AE$,$AF$分别是$\triangle ABC$的中线、角平分线和高,则下列各式中错误的是 (

A.$BC = 2CD$
B.$\angle BAE=\frac{1}{2}\angle BAC$
C.$\angle AFB = 90^{\circ}$
D.$AE = CE$
D
)
A.$BC = 2CD$
B.$\angle BAE=\frac{1}{2}\angle BAC$
C.$\angle AFB = 90^{\circ}$
D.$AE = CE$
答案:D
解析:
选项D之前的条件分析:
A选项:由于$AD$是中线,根据中线的定义它将$BC$分成两个等长的部分,即$BC=2CD$,故A选项正确。
B选项:由于$AE$是角平分线,根据角平分线的定义,它将$\angle BAC$分成两个相等的部分,即$\angle BAE=\frac{1}{2}\angle BAC$,故B选项正确。
C选项:由于$AF$是高,根据高的定义,它与$BC$垂直,即$\angle AFB=90°$,故C选项正确。
D选项:题目中并没有给出任何条件表明$AE=CE$,根据图形和题目中的信息,无法推导出$AE=CE$,故D选项错误。
因此,本题选择D。
A选项:由于$AD$是中线,根据中线的定义它将$BC$分成两个等长的部分,即$BC=2CD$,故A选项正确。
B选项:由于$AE$是角平分线,根据角平分线的定义,它将$\angle BAC$分成两个相等的部分,即$\angle BAE=\frac{1}{2}\angle BAC$,故B选项正确。
C选项:由于$AF$是高,根据高的定义,它与$BC$垂直,即$\angle AFB=90°$,故C选项正确。
D选项:题目中并没有给出任何条件表明$AE=CE$,根据图形和题目中的信息,无法推导出$AE=CE$,故D选项错误。
因此,本题选择D。
5. 下列说法中,正确的是 (
A.三角形的高、中线是线段,角平分线是射线
B.三角形的三条高中,至少有一条在三角形的内部
C.钝角三角形的三条角平分线在三角形的外部
D.连接三角形的一个顶点和它对边中点的直线叫作三角形的中线
B
)A.三角形的高、中线是线段,角平分线是射线
B.三角形的三条高中,至少有一条在三角形的内部
C.钝角三角形的三条角平分线在三角形的外部
D.连接三角形的一个顶点和它对边中点的直线叫作三角形的中线
答案:B
解析:
A. 三角形的高、中线、角平分线均为线段,故此选项错误。
B. 锐角三角形三条高在三角形内部;直角三角形一条高在三角形内部,另两条高为两直角边;钝角三角形一条高在三角形内部,另两条高在三角形外部。因此,至少有一条高在三角形内部,此选项正确。
C. 钝角三角形的三条角平分线均在三角形内部,故此选项错误。
D. 连接三角形的一个顶点和它对边中点的线段叫作三角形的中线,而不是直线,故此选项错误。
B. 锐角三角形三条高在三角形内部;直角三角形一条高在三角形内部,另两条高为两直角边;钝角三角形一条高在三角形内部,另两条高在三角形外部。因此,至少有一条高在三角形内部,此选项正确。
C. 钝角三角形的三条角平分线均在三角形内部,故此选项错误。
D. 连接三角形的一个顶点和它对边中点的线段叫作三角形的中线,而不是直线,故此选项错误。
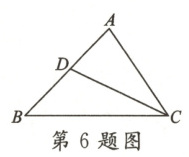
6. 如图,在$\triangle ABC$中,$CD$是中线,$BC - AC = 5\ cm$,$\triangle DBC$的周长为$25\ cm$,则$\triangle ADC$的周长是 (
A.$20\ cm$
B.$25\ cm$
C.$30\ cm$
D.$35\ cm$
A
)
A.$20\ cm$
B.$25\ cm$
C.$30\ cm$
D.$35\ cm$
答案:A
解析:
∵CD是△ABC的中线,∴AD=BD。
∵△DBC的周长为25cm,∴BD+BC+CD=25cm。
∵△ADC的周长=AD+AC+CD,AD=BD,∴△ADC的周长=BD+AC+CD。
∵BC - AC = 5cm,∴BC=AC+5。
∴BD+(AC+5)+CD=25cm,即BD+AC+CD=20cm。
∴△ADC的周长=20cm。
∵△DBC的周长为25cm,∴BD+BC+CD=25cm。
∵△ADC的周长=AD+AC+CD,AD=BD,∴△ADC的周长=BD+AC+CD。
∵BC - AC = 5cm,∴BC=AC+5。
∴BD+(AC+5)+CD=25cm,即BD+AC+CD=20cm。
∴△ADC的周长=20cm。
目录查找(点击展开或折叠章节目录)
切换年代卷册
X
