0 326842 326850 326856 326860 326866 326868 326872 326878 326880 326886 326892 326896 326898 326902 326908 326910 326916 326920 326922 326926 326928 326932 326934 326936 326937 326938 326940 326941 326942 326944 326946 326950 326952 326956 326958 326962 326968 326970 326976 326980 326982 326986 326992 326998 327000 327006 327010 327012 327018 327022 327028 327036 366461

 的长为
的长为 ;③点C为
;③点C为 的中点;④BD平分∠ADE.以上结论一定正确的是_________________.(把正确结论的序号都填上)
的中点;④BD平分∠ADE.以上结论一定正确的是_________________.(把正确结论的序号都填上) 的长=
的长=
 的中点.
的中点. .
. .
.


 , 并把解集在数轴上表示出来.
, 并把解集在数轴上表示出来.
 , 并把解集在数轴上表示出来.
, 并把解集在数轴上表示出来.
 ,
,




 根据点
根据点

 画出点
画出点


 用待定系数法求出函数解析式,即可求出对称轴方程.
用待定系数法求出函数解析式,即可求出对称轴方程. ;
;

 代入二次函数
代入二次函数 ,得
,得




 套用上面的归纳总结代入数据,即可得出结论;
套用上面的归纳总结代入数据,即可得出结论; 利用上面总结的结论套入数据表示出该两个两位数的成绩,在将等式展开合并同类项得出左边=右边,从而证明结论成立.
利用上面总结的结论套入数据表示出该两个两位数的成绩,在将等式展开合并同类项得出左边=右边,从而证明结论成立. 直接运算即可.
直接运算即可. )
)
 )
)
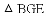
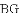
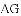
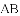
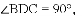
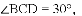
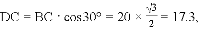
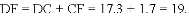
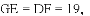
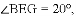
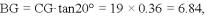
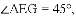
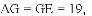
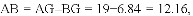


 ;(2)见解析
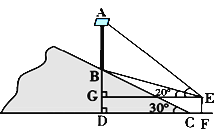
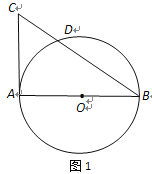
;(2)见解析 连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得
连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得
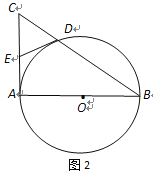
 连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到


 ;(2)
;(2)
 列举出将4名同学随机分成两组进行对打所有可能的结果,找出甲乙两人对打的情况数,根据概率公式计算即可.
列举出将4名同学随机分成两组进行对打所有可能的结果,找出甲乙两人对打的情况数,根据概率公式计算即可. 画树状图写出所有的情况,根据概率的求法计算概率.
画树状图写出所有的情况,根据概率的求法计算概率.

 .
.

 直接进行计算即可.
直接进行计算即可. 用待定系数法求一次函数解析式即可, 902班的要分成3段.
用待定系数法求一次函数解析式即可, 902班的要分成3段. 当x=2时,两班同学共植树150棵,
当x=2时,两班同学共植树150棵, 平均成本:不符合题意;,x>2,两班共植树(105x-60)棵.列出方程
平均成本:不符合题意;,x>2,两班共植树(105x-60)棵.列出方程 求解即可.
求解即可. (棵)
(棵)
 (x≥0),
(x≥0), ,
,
 ,
,

 B.
B.  C.
C.  D.
D. 