重庆市的重大惠民工程--公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积 单位:百万平方米
单位:百万平方米 ,与时间x的关系是
,与时间x的关系是 单位:年,
单位:年,  且x为整数
且x为整数 ;后4年,每年竣工投入使用的公租房面积
;后4年,每年竣工投入使用的公租房面积 单位:百万平方米
单位:百万平方米 ,与时间x的关系是
,与时间x的关系是 单位:年,
单位:年,  且x为整数
且x为整数 假设每年的公租房全部出租完
假设每年的公租房全部出租完 另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金
另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金 单位:元
单位:元 与时间
与时间 单位:年,
单位:年,  且x为整数
且x为整数 满足一次函数关系如下表:
满足一次函数关系如下表:
| 50 | 52 | 54 | 56 | 58 |
|
| 1 | 2 | 3 | 4 | 5 |
|
 求出z与x的函数关系式;
求出z与x的函数关系式;
 求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
 若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高
若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高 ,这样可解决住房的人数将比第6年减少
,这样可解决住房的人数将比第6年减少 ,求a的值.
,求a的值.
 参考数据:
参考数据: 
中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:

 根据上图填写下表:
根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | | | ______ | ______ |
乙班 | | ______ | 10 | |
 根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
 不妨设该种品牌玩具的销售单价为x元
不妨设该种品牌玩具的销售单价为x元 ,请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
,请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价 | x |
销售量 | ______ |
销售玩具获得利润 | ______ |
 在
在 问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
 在
在 问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
 ,再从
,再从 中选择一个合适的数代入求值.
中选择一个合适的数代入求值. 元
元

 年
年

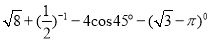 .
.



 求证:
求证:  ≌
≌ ;
; 连接
连接 ,当
,当 ______°和
______°和 ______°时,四边形ACED是正方形?请说明理由.
______°时,四边形ACED是正方形?请说明理由.

 方向以每小时15海里的速度航行,甲沿南偏西
方向以每小时15海里的速度航行,甲沿南偏西 方向以每小时
方向以每小时 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东 方向追赶乙船,正好在B处追上
方向追赶乙船,正好在B处追上 甲船追赶乙船的速度为多少海里
甲船追赶乙船的速度为多少海里 小时?
小时?
 元
元
 件
件
 元
元
 ,以点A为圆心,1为半径画
,以点A为圆心,1为半径画 与OA的延长线交于点C,过点A画OA的垂线,垂线与
与OA的延长线交于点C,过点A画OA的垂线,垂线与 的一个交点为B,连接BC
的一个交点为B,连接BC 线段BC的长等于______;
线段BC的长等于______; 请在图中按下列要求逐一操作,并回答问题:
请在图中按下列要求逐一操作,并回答问题: 以点______为圆心,以线段______的长为半径画弧,与射线BA交于点D,使线段OD的长等于
以点______为圆心,以线段______的长为半径画弧,与射线BA交于点D,使线段OD的长等于
 连OD,在OD上画出点P,使OP的长等于
连OD,在OD上画出点P,使OP的长等于 ,请写出画法,并说明理由.
,请写出画法,并说明理由.
 与x轴交于A、B两点,其中点
与x轴交于A、B两点,其中点 ,交y轴于点
,交y轴于点 直线
直线 过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点
过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点 不与点B、D重合
不与点B、D重合 ,过点P作y轴的平行线,交直线BD于点E,过点D作
,过点P作y轴的平行线,交直线BD于点E,过点D作 轴于点M.
轴于点M. 求抛物线
求抛物线 的表达式及点D的坐标;
的表达式及点D的坐标; 若四边形PEMN是平行四边形?请求出点P的坐标;
若四边形PEMN是平行四边形?请求出点P的坐标; 过点P作
过点P作 于点F,设
于点F,设 的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.
的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.