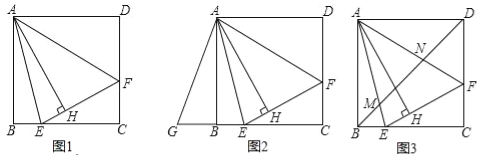
0 326222 326230 326236 326240 326246 326248 326252 326258 326260 326266 326272 326276 326278 326282 326288 326290 326296 326300 326302 326306 326308 326312 326314 326316 326317 326318 326320 326321 326322 326324 326326 326330 326332 326336 326338 326342 326348 326350 326356 326360 326362 326366 326372 326378 326380 326386 326390 326392 326398 326402 326408 326416 366461
 ≈1.41,
≈1.41,  ≈1.73)
≈1.73)
 米,所以警示牌的高CD=4
米,所以警示牌的高CD=4

 ,∴当
,∴当 棵时,橘子总个数最多.故答案为:10.
棵时,橘子总个数最多.故答案为:10.

 =
= ,即
,即 =
= ,又因BD=2DC,DC=DE,可得
,又因BD=2DC,DC=DE,可得 )÷(
)÷( ),其中a=2+
),其中a=2+ .
. )÷(
)÷( ),其中a=2+
),其中a=2+ .
. )÷(
)÷( )
) -
- )
) ·
·
 .
.
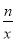 (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.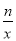 的解集.
的解集.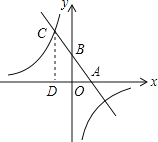
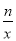 (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6. 的解集.
的解集.
 ;(2)(5,﹣4);(3)﹣2≤x<0或x≥5.
;(2)(5,﹣4);(3)﹣2≤x<0或x≥5.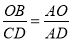 ,∴
,∴ ,∴CD=10,∴点C坐标(﹣2,10),B(0,6),A(3,0),∴
,∴CD=10,∴点C坐标(﹣2,10),B(0,6),A(3,0),∴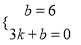 解得:
解得:  ,∴一次函数为y=﹣2x+6.
,∴一次函数为y=﹣2x+6.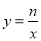 经过点C(﹣2,10),∴n=﹣20,∴反比例函数解析式为
经过点C(﹣2,10),∴n=﹣20,∴反比例函数解析式为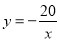 ;
; ,解得
,解得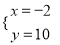 或
或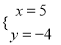 ,故另一个交点坐标为(5,﹣4);
,故另一个交点坐标为(5,﹣4);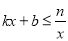 的解集:﹣2≤x<0或x≥5.
的解集:﹣2≤x<0或x≥5.


 =3/8.
=3/8.

 ×100%=32%,所以m=32.
×100%=32%,所以m=32. (4×5+16×10+12×15+10×20+8×30)=16(元),
(4×5+16×10+12×15+10×20+8×30)=16(元), =1.1,
=1.1,  =1.2,
=1.2,  =1.3,
=1.3,  =1.4)
=1.4)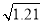 =1.1,
=1.1,  =1.2,
=1.2,  =1.3,
=1.3,  =1.4)
=1.4)