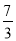0 326050 326058 326064 326068 326074 326076 326080 326086 326088 326094 326100 326104 326106 326110 326116 326118 326124 326128 326130 326134 326136 326140 326142 326144 326145 326146 326148 326149 326150 326152 326154 326158 326160 326164 326166 326170 326176 326178 326184 326188 326190 326194 326200 326206 326208 326214 326218 326220 326226 326230 326236 326244 366461
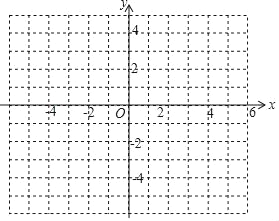
 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.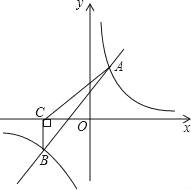
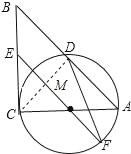
 ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.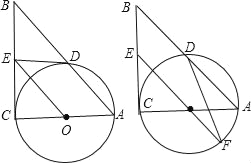
 ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.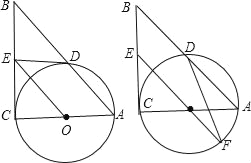
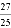
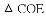
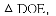
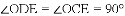
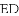
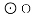
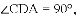
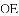
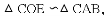
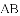
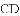
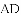
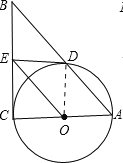
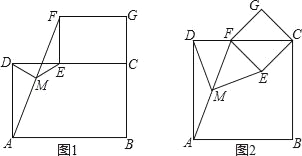
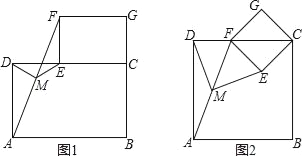
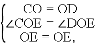 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),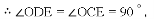
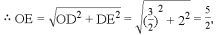
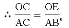 ∴AB=5,
∴AB=5,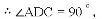
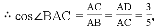
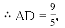
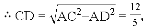
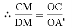
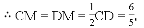
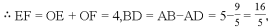
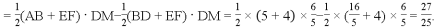
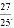
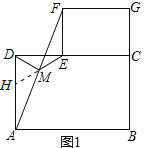
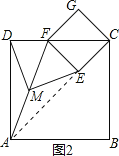
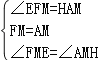


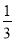 ,则这个数是( )
,则这个数是( )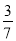 B. ﹣
B. ﹣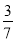 C.
C. 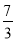 D. ﹣
D. ﹣