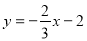0 325881 325889 325895 325899 325905 325907 325911 325917 325919 325925 325931 325935 325937 325941 325947 325949 325955 325959 325961 325965 325967 325971 325973 325975 325976 325977 325979 325980 325981 325983 325985 325989 325991 325995 325997 326001 326007 326009 326015 326019 326021 326025 326031 326037 326039 326045 326049 326051 326057 326061 326067 326075 366461
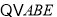 为等边三角形,
为等边三角形,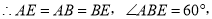
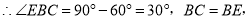
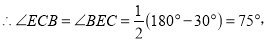
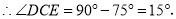
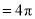 ,
,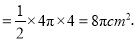
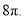
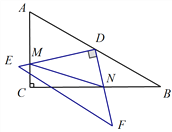
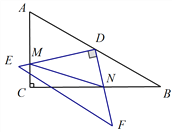
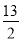
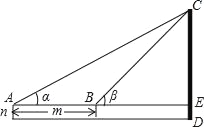
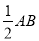 ,根据勾股定理求得AB=13,所以线段MN的最小值为
,根据勾股定理求得AB=13,所以线段MN的最小值为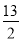 .
.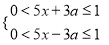 ,其中a为参数.
,其中a为参数.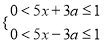 ,其中a为参数.
,其中a为参数.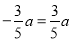 时、当
时、当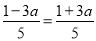 时、当
时、当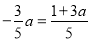 时、当
时、当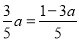 时a的值,结合不等式的解集,即可求出在各段的不等式组的解集.
时a的值,结合不等式的解集,即可求出在各段的不等式组的解集.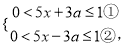
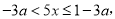
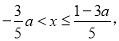
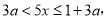
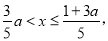
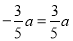 时,a=0,
时,a=0,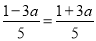 时,a=0,
时,a=0,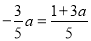 时,
时, 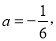
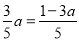 时,
时, 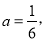
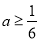 或
或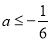 时,原不等式组无解;
时,原不等式组无解;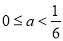 时,原不等式组的解集为
时,原不等式组的解集为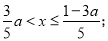
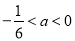 时,原不等式组的解集为:
时,原不等式组的解集为: 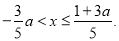
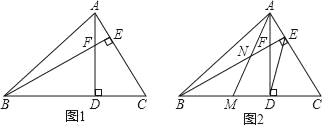
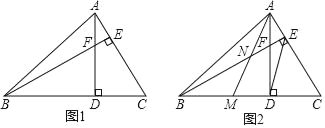
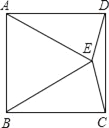
 AC,理由见解析.
AC,理由见解析. AC.
AC.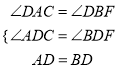 ,
,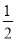 AC,理由是:
AC,理由是: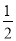 AC.
AC. n(n+4)=0的两根,且(x1﹣1)(x2﹣1)﹣1=
n(n+4)=0的两根,且(x1﹣1)(x2﹣1)﹣1=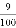 ,求n的值.
,求n的值. n(n+4)=0的两根,且(x1﹣1)(x2﹣1)﹣1=
n(n+4)=0的两根,且(x1﹣1)(x2﹣1)﹣1=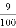 ,求n的值.
,求n的值.
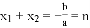 ①,
①,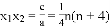 ②,再把①②代入
②,再把①②代入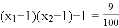 中,可求出n的值,再根据根的判别式,可求出n的取值范围,最终可确定n的值.
中,可求出n的值,再根据根的判别式,可求出n的取值范围,最终可确定n的值.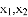 是方程
是方程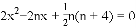 的两根,
的两根,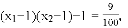
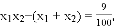 把①②代入上式得
把①②代入上式得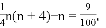 化简得
化简得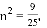 即
即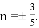
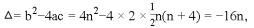
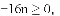
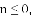
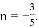
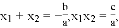
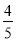 ,问甲、乙两公司人均捐款各多少元?
,问甲、乙两公司人均捐款各多少元?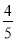 ,问甲、乙两公司人均捐款各多少元?
,问甲、乙两公司人均捐款各多少元?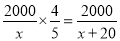
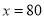
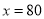 为原方程的根, 80+20=100
为原方程的根, 80+20=100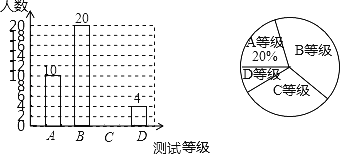
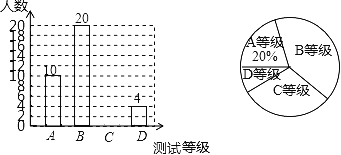
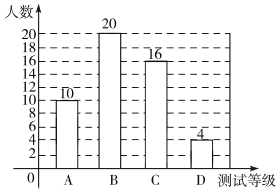
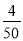 =56(名)
=56(名)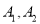 ,体能为A等级的两名女生分别为
,体能为A等级的两名女生分别为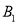 ,
,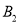 ,画树状图如下:
,画树状图如下: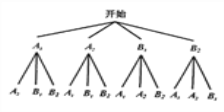
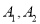 ),(
),(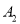 ,
,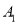 ), ∴P(抽取的两人是男生)=
), ∴P(抽取的两人是男生)=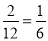 .
.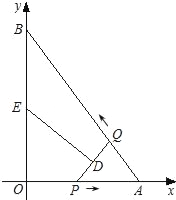
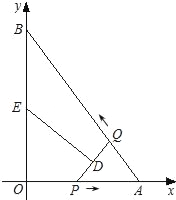
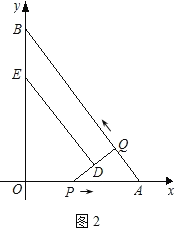
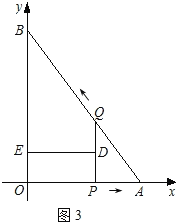
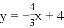 ;(2)S=﹣
;(2)S=﹣ t2+
t2+ t;
t;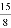 ;②当DE经过点O时,t=
;②当DE经过点O时,t= 或
或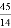 .
.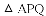
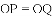
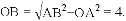
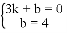 .解得
.解得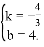
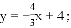
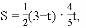
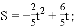
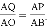
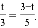
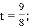
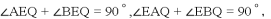
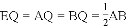
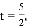
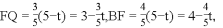
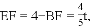
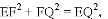
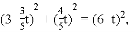
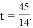
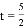 或
或
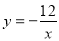 一次函数:
一次函数: