0 325880 325888 325894 325898 325904 325906 325910 325916 325918 325924 325930 325934 325936 325940 325946 325948 325954 325958 325960 325964 325966 325970 325972 325974 325975 325976 325978 325979 325980 325982 325984 325988 325990 325994 325996 326000 326006 326008 326014 326018 326020 326024 326030 326036 326038 326044 326048 326050 326056 326060 326066 326074 366461
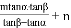 )米.
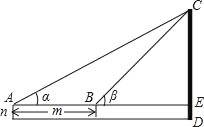
)米.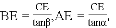 由AE?BE=AB=m米,可得
由AE?BE=AB=m米,可得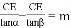 ,继而可求得CE的长,又由测角仪的高度是
,继而可求得CE的长,又由测角仪的高度是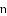
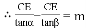 (米),
(米),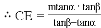 (米),
(米),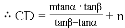 (米).
(米).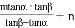 米
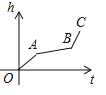
米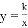 (k>0)刻画(如图所示).
(k>0)刻画(如图所示).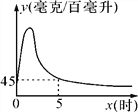
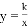 (k>0)刻画(如图所示).
(k>0)刻画(如图所示).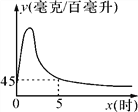
 (k>0), ∴k=xy=45×5=225;
(k>0), ∴k=xy=45×5=225;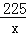 ,则y=
,则y=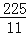 >20, ∴第二天早上7:00不能驾车去上班.
>20, ∴第二天早上7:00不能驾车去上班.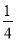 x2﹣
x2﹣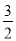 x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.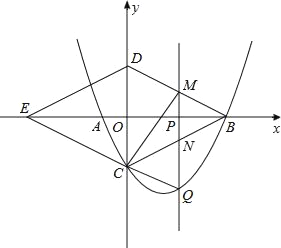
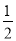 B.
B. 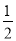 C. ﹣2 D. 2
C. ﹣2 D. 2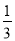 ,y=4,则代数式3x+y﹣3的值为( )
,y=4,则代数式3x+y﹣3的值为( )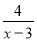 有意义,x应满足的条件是( )
有意义,x应满足的条件是( )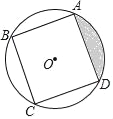
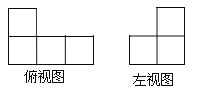
 B.
B. C.
C. D.
D.
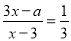 的解是非负数,那么a的取值范围是( )
的解是非负数,那么a的取值范围是( )