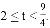0 325842 325850 325856 325860 325866 325868 325872 325878 325880 325886 325892 325896 325898 325902 325908 325910 325916 325920 325922 325926 325928 325932 325934 325936 325937 325938 325940 325941 325942 325944 325946 325950 325952 325956 325958 325962 325968 325970 325976 325980 325982 325986 325992 325998 326000 326006 326010 326012 326018 326022 326028 326036 366461
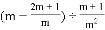 ,其中m是方程x2+x﹣3=0的根.
,其中m是方程x2+x﹣3=0的根.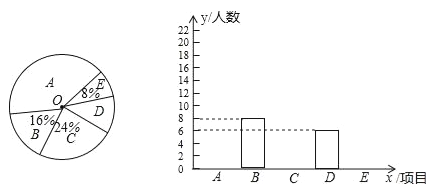
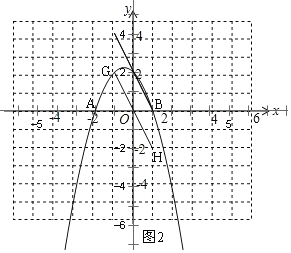
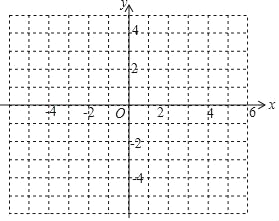
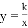 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题: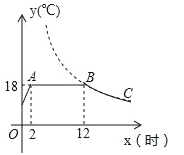
 ,﹣
,﹣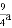 );(2)
);(2)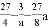 ;(3) 2≤t<
;(3) 2≤t< .
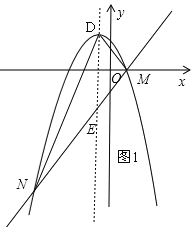
.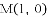 代入直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,可求得另一交点N的坐标,根据a<b,判断a<0,确定D、M、N的位置,画图1,根据面积和可得
代入直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,可求得另一交点N的坐标,根据a<b,判断a<0,确定D、M、N的位置,画图1,根据面积和可得
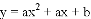 有一个公共点M(1,0),
有一个公共点M(1,0),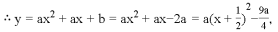
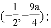
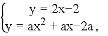
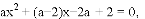
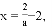
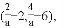
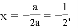
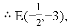
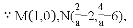
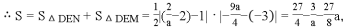
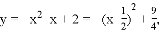
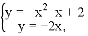
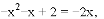
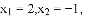
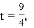 当点H平移后落在抛物线上时,坐标为(1,0),
当点H平移后落在抛物线上时,坐标为(1,0),