16. 如图,已知AB=AC,AD平分∠BAC,那么就可以证明△ABD≌△ACD,理由是( )
如图,已知AB=AC,AD平分∠BAC,那么就可以证明△ABD≌△ACD,理由是( )
 如图,已知AB=AC,AD平分∠BAC,那么就可以证明△ABD≌△ACD,理由是( )
如图,已知AB=AC,AD平分∠BAC,那么就可以证明△ABD≌△ACD,理由是( )| A. | SSS | B. | ASA | C. | SAS | D. | AAS |
15.在△ABC中,∠C=80°,∠B=60°,那么∠A的度数是( )
| A. | 20° | B. | 40° | C. | 60° | D. | 70° |
14.下列几种车的标志中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.函数y=x2+x-6的图象与y轴交点的纵坐标是( )
| A. | -4 | B. | -4 | C. | 0 | D. | -6 |
10.Rt△ABC中,直角边AC=1,BC=2,则斜边AB的长度大约是( )
| A. | 在2和3之间 | B. | 在3和4之间 | C. | 在4和5之间 | D. | 在5和6之间 |
9.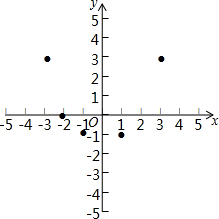 有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.
有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.
小峰根据学习函数的经验,对函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质进行了探究.
下面是小峰的探究过程,请补充完整:
(1)函数y=x2-2$\sqrt{{x}^{2}}$的自变量的取值范围是任意实数;
(2)下表是y与x的几组对应值.
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第四象限内的最低点是(1,-1),结合函数的图象,写出该函数的其它性质(一条即可):对称轴是y轴.
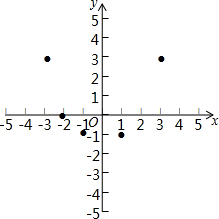 有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.
有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.小峰根据学习函数的经验,对函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质进行了探究.
下面是小峰的探究过程,请补充完整:
(1)函数y=x2-2$\sqrt{{x}^{2}}$的自变量的取值范围是任意实数;
(2)下表是y与x的几组对应值.
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | n | 3 | 0 | -1 | 0 | -1 | 0 | 3 | m | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第四象限内的最低点是(1,-1),结合函数的图象,写出该函数的其它性质(一条即可):对称轴是y轴.
7.下列各图中,是中心对称图形的为( )
0 312527 312535 312541 312545 312551 312553 312557 312563 312565 312571 312577 312581 312583 312587 312593 312595 312601 312605 312607 312611 312613 312617 312619 312621 312622 312623 312625 312626 312627 312629 312631 312635 312637 312641 312643 312647 312653 312655 312661 312665 312667 312671 312677 312683 312685 312691 312695 312697 312703 312707 312713 312721 366461
| A. |  | B. |  | C. |  | D. |  |
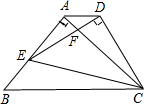 如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,下列说法:①AC⊥ED;②∠BCE=∠ACD;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD面积的最大值为$\frac{3}{8}$,其中正确的是②④⑤.
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,下列说法:①AC⊥ED;②∠BCE=∠ACD;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD面积的最大值为$\frac{3}{8}$,其中正确的是②④⑤.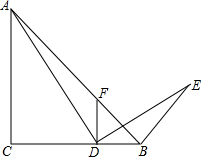 如图,在△ABC中,∠C=90°,AC=BC,点D在BC边上,连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE,作DF⊥BC交AB于点F.
如图,在△ABC中,∠C=90°,AC=BC,点D在BC边上,连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE,作DF⊥BC交AB于点F.