10.若a是有理数,则下列判断正确的是( )
| A. | |a|是正数 | B. | -a是负数 | C. | |a|是正数或0 | D. | |-a|是负数或0 |
8.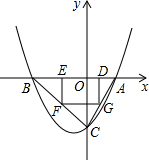 如图,已知抛物线T:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线T上部分点的横坐标对应的纵坐标如下:
如图,已知抛物线T:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线T上部分点的横坐标对应的纵坐标如下:
(1)写出A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值m时
①抛物线T上是否存在点P,使S△PBC=m?若存在,请求出P点坐标;若不存在,请说明理由.
②连接DF并延长至点M,使FM=k•DF,若点M不在抛物线T上,求k的取值范围.
 如图,已知抛物线T:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线T上部分点的横坐标对应的纵坐标如下:
如图,已知抛物线T:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线T上部分点的横坐标对应的纵坐标如下:| x | … | -3 | -2 | 1 | 2 | … |
| y | … | -$\frac{5}{2}$ | -4 | -$\frac{5}{2}$ | 0 | … |
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值m时
①抛物线T上是否存在点P,使S△PBC=m?若存在,请求出P点坐标;若不存在,请说明理由.
②连接DF并延长至点M,使FM=k•DF,若点M不在抛物线T上,求k的取值范围.
4.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与 CD1交于点O,则线段AD1的长为( )
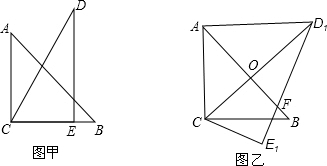

| A. | 6$\sqrt{2}$ | B. | 10 | C. | 8 | D. | $\sqrt{31}$ |
1.用公式法解方程x2-x=2时,求根公式中的a,b,c的值分别是( )
0 312485 312493 312499 312503 312509 312511 312515 312521 312523 312529 312535 312539 312541 312545 312551 312553 312559 312563 312565 312569 312571 312575 312577 312579 312580 312581 312583 312584 312585 312587 312589 312593 312595 312599 312601 312605 312611 312613 312619 312623 312625 312629 312635 312641 312643 312649 312653 312655 312661 312665 312671 312679 366461
| A. | a=1,b=1,c=2 | B. | a=1,b=-1,c=-2 | C. | a=1,b=1,c=-2 | D. | a=1,b=-1,c=2 |
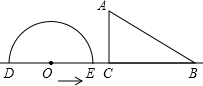 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的左侧,OC=8cm.(提示:直角三角形中,30度所对的直角边是斜边的一半,反之成立)
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的左侧,OC=8cm.(提示:直角三角形中,30度所对的直角边是斜边的一半,反之成立) 一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数:y=-$\frac{1}{20}$x+8.
一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数:y=-$\frac{1}{20}$x+8.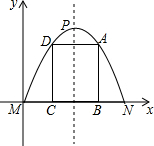 如图,有一块铁皮,拱形边缘呈抛物线状,MN=4dm,抛物线顶点到MN的距离是4dm.要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在MN上,A、D落在抛物线上.建立如图所示的平面直角坐标系,
如图,有一块铁皮,拱形边缘呈抛物线状,MN=4dm,抛物线顶点到MN的距离是4dm.要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在MN上,A、D落在抛物线上.建立如图所示的平面直角坐标系,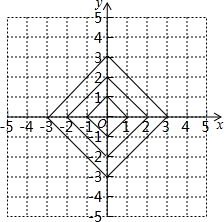 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,如图,由里向外数的第2各正方形开始,分别是由第1个正方形各顶点的横坐标和纵坐标分别乘1,2,3,…得到的,请你观察图形,猜想由里向外第12个正方形四条边上的整点个数为48.
在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,如图,由里向外数的第2各正方形开始,分别是由第1个正方形各顶点的横坐标和纵坐标分别乘1,2,3,…得到的,请你观察图形,猜想由里向外第12个正方形四条边上的整点个数为48. 如图,一只蚂蚁以均匀的速度沿台阶A→B→C→D→E爬行,那么蚂蚁爬行的高度h与时间t的函数图象大致是( )
如图,一只蚂蚁以均匀的速度沿台阶A→B→C→D→E爬行,那么蚂蚁爬行的高度h与时间t的函数图象大致是( )



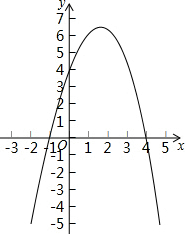 已知二次函数y=-x2+3x+4的图象如图:(直接写答案)
已知二次函数y=-x2+3x+4的图象如图:(直接写答案)